Cho hình lăng trụ $\large ABC.A'B'C'$ có đáy $\large ABC$ là tam giác

Cho hình lăng trụ $\large ABC.A'B'C'$ có đáy $\large ABC$ là tam giác vuông cân tại $\large A$, cạnh $\large AC=2\sqrt{2}$. Biết $\large AC'$ tạo với mặt phẳng $\large (ABC)$ một góc $\large 60^{\circ}$ và $\large AC'=4$. Thể tích của khối đa diện $\large ABCB'C'$ bằng:

• A.

  A. $\large\dfrac{8}{3}$

• B.

  B. $\large\dfrac{16}{3}$

• C.

  C. $\large\dfrac{8\sqrt{3}}{3}$

• D.

  D. $\large\dfrac{16\sqrt{3}}{3}$

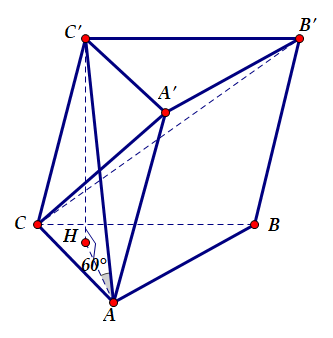
Chiều cao khối lăng trụ: $\large h=AC'.\sin 60^{\circ}=2\sqrt{3}$

Thể tích khối lăng trụ: $\large V_{ABC.A'B'C'}=S_{\bigtriangleup ABC}.h=\dfrac{1}{2}AC^{2}.h=8\sqrt{3}$

Suy ra thể tích cần tính: $\large V_{ABCB'C'}=\dfrac{2}{3}V_{ABC.A'B'C'}=\dfrac{16\sqrt{3}}{3}$

Đáp án D