Cho hình hộp chữ nhật $\Large ABCD.A'B'C'D'$ có $\Large AB=a\sqrt{3}$

Cho hình hộp chữ nhật $\Large ABCD.A'B'C'D'$ có $\Large AB=a\sqrt{3}$ và $\Large AD=a.$ Góc giữa hai đường thẳng $\Large B'D'$ và $\Large AC$ bằng

• A.

  A. $\Large 45^{\circ}.$

• B.

  B. $\Large 60^{\circ}.$

• C.

  C. $\Large 90^{\circ}.$

• D.

  D. $\Large 30^{\circ}.$

Chọn B.

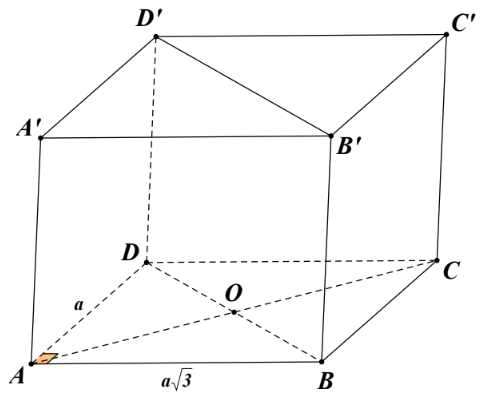
Vì $\Large ABCD.A'B'C'D'$ là hình hộp chữ nhật nên $\Large BD// {B}'{D}'$ suy ra $\Large \widehat{\big({B}'{D}', AC \big)}=\widehat{\big(BD,AC\big)}.$

$\Large ABCD$ là hình chữ nhật có $\Large AB=a\sqrt{3}$ và $\Large AD=a$ nên $\Large BD=\sqrt{AB^2+AD^2}=2a=AC$

$\Large \Rightarrow OD=OA=a=AD$

$\Large \Delta OAD$ là tam giác đều $\Large \Rightarrow \widehat{AOD}=60^{\circ}.$

Vậy $\Large \widehat{\big({B}'{D}', AC\big)}=\widehat{\big(BD, AC\big)}=\widehat{AOD}=60^{\circ}.$