Cho hình chóp tứ giác đều $\Large S.ABCD$ có cạnh đáy bằng $\Large a$

Cho hình chóp tứ giác đều $\Large S.ABCD$ có cạnh đáy bằng $\Large a$ và góc giữa mặt bên và mặt phẳng đáy bằng $\Large 45^{o}$. Diện tích mặt cầu ngoại tiếp hình chóp $\Large S.ABCD$ là:

• A.

  A. $\Large \dfrac{4 \pi a^{2}}{3}$

• B.

  B. $\Large \dfrac{3 \pi a^{2}}{4}$

• C.

  C. $\Large \dfrac{2 \pi a^{2}}{3}$

• D.

  D. $\Large \dfrac{9 \pi a^{2}}{4}$

Chọn D

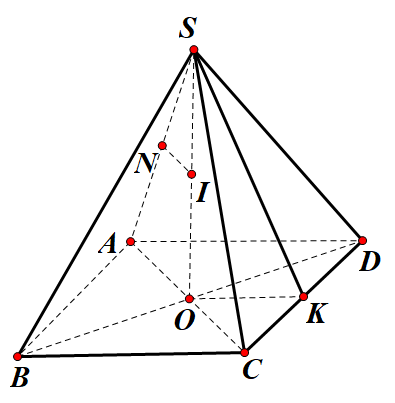
Gọi $\Large O$ là tâm của đáy suy ra $\Large SO$ là trục của đường tròn ngoại tiếp đáy đa giác.

Từ $\Large O$ dựng $\Large OK$ vuông góc với $\Large BC$, suy ra $\Large K$ là trung điểm $\Large BC$.

Xét tam giác $\Large SBC$ cân tại $\Large S$ có $\Large SK \bot BC$.

Từ đó ta có $\Large \left\{\begin{array}{l} SK \bot BC \\ OK \bot BC \\ \end{array}\right.$

=> Góc giữa mặt phẳng $\Large SBC$ và mặt phẳng đáy $\Large ABCD$ là góc $\Large SKO$.

Xét tam giác $\Large OBC$ vuông cân tại $\Large O$ có $\Large OK = \dfrac{1}{2}BC = \dfrac{a}{2}$.

Xét tam giác $\Large SKO$ vuông tại $\Large O$ có $\Large SO = OK . \tan SKO = \dfrac{a}{2}. \tan 45^{o} = \dfrac{a}{2}$.

Mặt khác:

$\Large SA^{2} = SO^{2} + OA^{2} = \left ( \dfrac{a}{2} \right )^{2} + \left ( \dfrac{a\sqrt{2}}{2} \right )^{2} = \dfrac{3a^{2}}{4}$

$\Large \Rightarrow SA = \dfrac{a\sqrt{3}}{2}$

Gọi $\Large N$ là trung điểm $\Large SA$. Trong mặt phẳng $\Large SAO$ vẽ đường trung trực của cạnh $\Large SA$ cắt $\Large SO$ tại $\Large I$, suy ra $\Large I$ là tâm mặt cầu ngoại tiếp hình chóp $\Large S.ABCD$.

Xét hai tam giác đồng dạng $\Large SNI$ và $\Large SOA$ có $\Large \dfrac{SN}{SO} = \dfrac{SI}{SA}$.

$\Large R = SI = \dfrac{SN . SA}{SO}= \dfrac{SA^{2}}{2.SO}= \dfrac{\left ( \dfrac{a\sqrt{3}}{2} \right )^{2}}{2\dfrac{a}{2}} = \dfrac{3a}{4}$.

Diện tích mặt cầu ngoại tiếp hình chóp $\Large S.ABCD$ là:

$\Large S = 4 \pi R^{2} = 4 \pi .\left ( \dfrac{3a}{4} \right )^{2} = \dfrac{9\pi a^{2}}{4}$.