Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy

Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA vuông góc với đáy, SC tạo với mặt phẳng (SAB) một góc $\large 30^\circ$. Tính thể tích khối chóp S.ABCD

• A.

  A. $\large \dfrac{\sqrt{2}}{3}a^3$

• B.

  B. $\large \dfrac{2}{3}a^3$

• C.

  C. $\large \sqrt{2}a^3$

• D.

  D. $\large \dfrac{\sqrt{6}}{3}a^3$

Chọn A

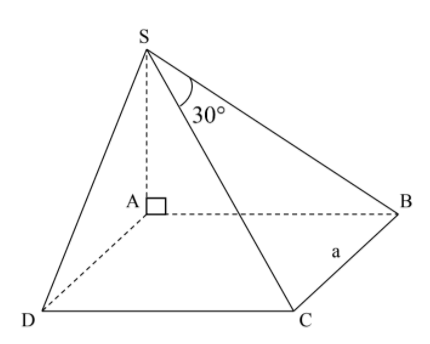
Ta có góc giữa SC và mặt phẳng (SAB) là góc CSB

Xét tam giác CSB vuông tại B, suy ra: $\large CSB=\dfrac{BC}{SB}\Rightarrow SB=\dfrac{BC}{\tan CSB}=\dfrac{a}{\tan 30^\circ}=a\sqrt{3}$

Tam giác SAB vuông tại A, áp dụng định lí Pytago ta được: 

$\large SA=\sqrt{SB^2-AB^2}=\sqrt{(a\sqrt{3})^2-a^2}=a\sqrt{2}$

Suy ra: $\large V_{S.ABCD}=\dfrac{1}{3}S_{ABCD}.SA=\dfrac{1}{3}.a^2.a\sqrt{2}=a^3.\dfrac{\sqrt{2}}{3}$