Trong không gian Oxyz, cho hai đường thẳng $\large d:\,\, \left\{\begi

Trong không gian Oxyz, cho hai đường thẳng $\large d:\,\, \left\{\begin{align}& x=2+3t\\& y=-3+t\\& z=4-2t\\\end{align}\right.$ và $\large d':\,\, \dfrac{x-4}{3}=\dfrac{y+1}{1}=\dfrac{z}{-2}$. Phương trình nào dưới đây là phương trình đường thẳng thuộc mặt phẳng chứa d và d' đồng thời cách đều hai đường thẳng đó: 

• A. A. $\large \dfrac{x-3}{3}=\dfrac{y-2}{1}=\dfrac{z-2}{-2}$
• B. B. $\large \dfrac{x+3}{3}=\dfrac{y+2}{1}=\dfrac{z+2}{-2}$
• C. C. $\large \dfrac{x-3}{3}=\dfrac{y+2}{1}=\dfrac{z-2}{-2}$
• D. D. $\large \dfrac{x+3}{3}=\dfrac{y-2}{1}=\dfrac{z+2}{-2}$

Chọn C

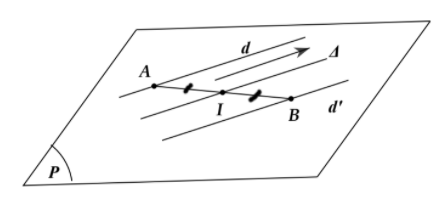
Vì hai đường thẳng d và d' có cùng vecto chỉ phương $\large \vec{u} (3; 1; -2)$ nên d và d' song song hoặc d và d' trùng nhau

Lấy $\large A(2; -3; 4)\in d$ thay vào phương trình đường thẳng d' không thỏa mãn suy ra $\large A(2; -3; 4)\notin D$ nên $\large d//d'$

Vì hai đường thẳng d và d' song song với nhau nên cùng nằm trên một mặt phẳng

Đường thẳng $\large \Delta $ cần tìm thuộc mặt phẳng chứa d và d' đồng thời cách đều hai đường thẳng đó thì cũng song song với hai đường thẳng s và d'. Do đó: $\large \Delta $ nhận vecto $\large \vec{u}(3; 1; -2)$ làm vecto chỉ phương 

Lấy $\large A(2; -3; 4)\in d; \,\, B(4; -1; 0)\in d'$. Gọi là trung điểm của AB $\large \Rightarrow I(3; -2; 2)\in \Delta$

Đường thẳng $\large \Delta$ cần tìm qua I(3; -2; -2) và nhận vecto $\large \vec{u} (3; 1; -2)$ làm vecto chỉ phương có phương trình $\large\dfrac{x-3}{3}=\dfrac{y+2}{1}=\dfrac{z-2}{-2} $