Cho hình chóp S.ABC có ABC là tam giác vuông cân tại B và $\Large BC=a

MỤC LỤC
Câu hỏi:
Cho hình chóp S.ABC có ABC là tam giác vuông cân tại B và $\Large BC=a.$ Cạnh bên SA vuông góc với đáy (ABC). Gọi H, K lần lượt là hình chiếu vuông góc của A lên SB và SC. Thể tích của khối cầu ngoại tiếp hình chóp A.HKCB bằng
Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
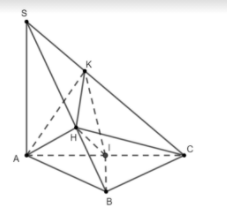
Gọi I là trung điểm của AC. Do tam giác ABC vuông cân tại B nên $\Large IA=IB=IC=\dfrac{1}{2}AC.$
Do $\Large AK\perp SC$ nên $\Large \Delta AKC$ vuông tại K, khi đó $\Large IA=IK=IC=\dfrac{1}{2}AC.$
Ta có $\Large BC\perp AB, BC \perp SA \Rightarrow BC \perp (SAB) \Rightarrow BC \perp AH,$ mà $\Large AH\perp SB$ nên $\Large AH \perp (SBC)$
$\Large \Rightarrow AH \perp HC$ hay $\Large \Delta AHC$ vuông tại H $\Large \Rightarrow IH=IA=IC=\dfrac{1}{2}AC.$
Như vậy $\Large IA=IB=IC=IH=IK=\dfrac{1}{2}AC$ hay mặt cầu ngoại tiếp hình chóp A.HKCB có tâm I là trung điểm AC, bán kính $\Large R=\dfrac{1}{2}AC=\dfrac{1}{2}BC\sqrt{2}=\dfrac{a\sqrt{2}}{2}.$
Vậy thể tích khối cầu là $\Large V=\dfrac{4}{3}\pi R^3=\dfrac{4}{3}\pi \left(\dfrac{a\sqrt{2}}{2}\right)^3=\dfrac{\sqrt{2}\pi a^3}{3}.$
Xem thêm các bài tiếp theo bên dưới
- Cho hàm số $\Large f(x)$ có đạo hàm liên tục trên $\Large \mathbb{R}$
- Cho hàm số $\Large f(x)=ax^3+bx^2+cx+d$ (với $\Large a, b, c, d \in \m
- Trong không gian Oxyz cho điểm đường thẳng $\Large d: \dfrac{x}{-2}=\d
- Cho hai số phức $\Large z_1=1-i$ và $\Large z_2=2+3i.$ Phần ảo của số
- Cho hàm số f(x) liên tục trên $\Large \mathbb{R}$ và $\Large \int\limi