Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABC$ là tam giác vuông tạ

Cho hình chóp $\Large S.ABCD$ có đáy $\Large ABC$ là tam giác vuông tại $\Large A,$ $\Large BC=a, \widehat{ABC}=30^{\circ}.$ Hai mặt bên $\Large (SAB)$ và $\Large (SAC)$ cùng vuông góc với mặt phẳng đáy, mặt bên $\Large (SBC)$ tạo với đáy một góc $\Large 45^{\circ}.$ Thể tích của khối chóp $\Large S.ABC$ là

• A.

  A. $\Large \dfrac{a^3}{32}.$

• B.

  B. $\Large \dfrac{a^3}{9}.$

• C.

  C. $\Large \dfrac{a^3}{16}.$

• D.

  D. $\Large \dfrac{a^3}{64}.$

Chọn A

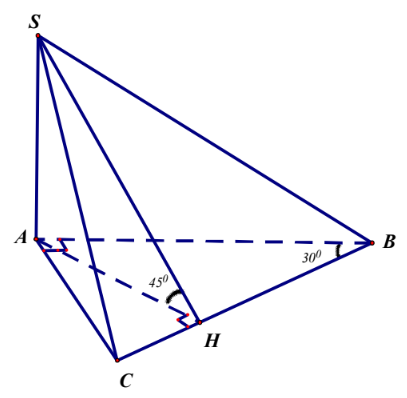
Ta có: Hai mặt bên $\Large (SAB)$ và $\Large (SAC)$ cùng vuông góc với mặt phẳng đáy nên ta có $\Large SA \perp (ABC),$ do đó $\Large SA$ là đường cao của hình chóp.

Từ $\Large A,$ kẻ $\Large AH \perp BC$ thì ta có $\Large SH\perp BC.$

Do $\Large \left\{\begin{align} & (SBC) \cap (ABC) =BC \\ & AH \subset (ABC), AH \perp BC \\ & SH \subset (SBC), SH \perp BC \end{align}\right.$ $\Large \Rightarrow \widehat{\big((SBC), (ABC)\big)}=\widehat{\left( SH, AH \right) }=\widehat{SHA}=45^{\circ}.$

Tam giác $\Large ABC$ là tam giác vuông tại $\Large A$ nên ta có

$\Large AB=BC.\cos\widehat{ABC}=a.\cos 30^{\circ}=\dfrac{a\sqrt{3}}{2}.$

$\Large AC=BC.\sin\widehat{ABC}=a.\sin 30^{\circ}=\dfrac{a}{2}.$

Có $\Large \dfrac{1}{AH^2}=\dfrac{1}{AC^2}+\dfrac{1}{AB^2}$ $\Large =\dfrac{1}{\bigg(\dfrac{a}{2}\bigg)^2}+\dfrac{1}{\bigg(\dfrac{a\sqrt{3}}{2}\bigg)^2}$ $\Large =\dfrac{4}{a^2}+\dfrac{4}{3a^2}$ $\Large =\dfrac{16}{3a^2}$

$\Large \Rightarrow AH=\dfrac{a\sqrt{3}}{4}$

Do $\Large SAH$ là tam giác vuông cân tại $\Large A$ nên ta có $\Large SA=AH=\dfrac{a\sqrt{3}}{4}.$

Từ đây ta suy ra $\Large V_{S.ABC}=\dfrac{1}{3}.SA.S_{\Delta ABC}$ $\Large =\dfrac{1}{3}.SA.\dfrac{1}{2}.AC.AB$ $\Large =\dfrac{1}{3}.\dfrac{a\sqrt{3}}{4}.\dfrac{1}{2}.\dfrac{a}{2}.\dfrac{a\sqrt{3}}{2}$ $\Large =\dfrac{a^3}{32} (dvtt).$