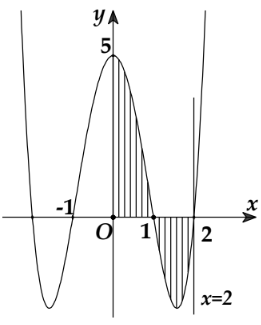
Cho hàm số $\Large y=f(x)=x^4-5x^2+4$ có đồ thị như hình vẽ bên. Gọi $

Cho hàm số $\Large y=f(x)=x^4-5x^2+4$ có đồ thị như hình vẽ bên. Gọi $\Large S$ là diện tích hình phẳng giới hạn bởi đồ thị hàm số $\Large y=f(x),$ trục hoành và hai đường thẳng $\Large x=0, x=2$ (miền phẳng được gạch chéo trong hình vẽ). Mệnh đề nào sau đây sai?

• A.

  $\Large S=\int\limits_0^2|f(x)|\mathrm{d}x.$

• B.

  $\Large S=\int\limits_0^1f(x)\mathrm{d}x-\int\limits_1^2f(x)\mathrm{d}x.$

• C.

  $\Large S=\Bigg|\int\limits_0^1f(x)\mathrm{d}x\Bigg|+\Bigg|\int\limits_1^2f(x)\mathrm{d}x\Bigg|.$

• D.

  $\Large S=\Bigg|\int\limits_0^2f(x)\mathrm{d}x\Bigg|.$

Chọn D

Diện tích hình phẳng giới hạn bởi đồ thị hàm số $\Large y=f(x),$ trục hoành và hai đường thẳng $\Large x=0, x=2$ được tính bởi công thức

$\Large S=\int\limits_0^2|f(x)|\mathrm{d}x=\int\limits_0^1|f(x)|\mathrm{d}x+\int\limits_1^2|f(x)|\mathrm{d}x.$

$\Large \Rightarrow S=\Bigg|\int\limits_0^1f(x)\mathrm{d}x\Bigg|+\Bigg|\int\limits_1^2f(x)\mathrm{d}x\Bigg|$

$\Large \Rightarrow S=\int\limits_0^1f(x)\mathrm{d}x-\int\limits_1^2f(x)\mathrm{d}x.$

Vậy $\Large S=\Bigg|\int\limits_0^2f(x)\mathrm{d}x\Bigg|$ là phương án sai.