Cho hàm số $\large y=f(x)$ xác định trên $\large \mathbb{R}\setminus \

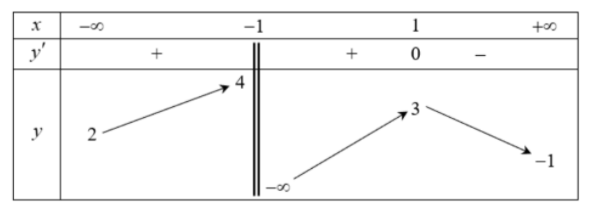
Cho hàm số $\large y=f(x)$ xác định trên $\large \mathbb{R}\setminus \left \{ 1 \right \}$, liên tục trên mỗi khoảng xác định và có bảng biến thiên như sau:

Hỏi đồ thị hàm số có tất cả bao nhiêu tiệm cận đứng và tiệm cận ngang?

• A. A. 1
• B. B. 0
• C. C. 2
• D. D. 3

Chọn D

Ta có: 

+) $\large \underset{x\to (-1)^+}{lim}\,\, y=-\infty$ nên đồ thị hàm số có 1 tiệm cận đứng là: $\large x=-1$

+) $\large \underset{x\to -\infty}{lim}\,\, y=2$ và $\large \underset{x\to +\infty}{lim}\,\, y=-1$ nên đồ thị hàm số có hai đường tiệm cận ngang là $\large y=2$ và $\large y=-1$

Vậy đồ thị hàm số có số đường tiệm cận đứng và tiệm cận ngang là 3