Cho hàm số $\large y=f(x)$ liên tục trên $\large \mathbb{R}$ và có đồ

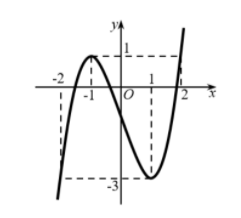
Cho hàm số $\large y=f(x)$ liên tục trên $\large \mathbb{R}$ và có đồ thị như hình vẽ. Phương trình $\large f(f(x)-1)=0$ có tất cả bao nhiêu nghiệm thực phân biệt? 

• A. 6
• B. 5
• C. 7
• D. 4

Chọn C

Từ đồ thị hàm số $\large y=f(x)$ suy ra $\large f(x)=0\Leftrightarrow $ $\large \left[\begin{align}& x=a\in (-2; -1)\\& x=b\in (-1; 0)\\& x=c\in (1; 2)\\\end{align}\right. $

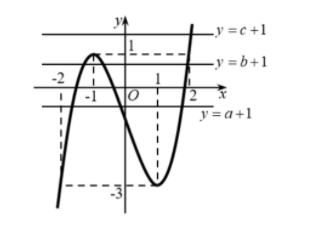
Suy ra: $\large f(f(x)-1)=0\Leftrightarrow $ $\large \left[\begin{align}& f(x)-1=a\\& f(x)-1=b\\& f(x)-1=c\\\end{align}\right. $ $\large \left[\begin{align}& f(x)=a+1\\& f(x)=b+1\\& f(x)=c+1\\\end{align}\right. $ 

+ Do $\large a\in (-2; -1)\Rightarrow a+1\in (-1; 0)\Rightarrow $ Phương trình $\large f(x)=a+1$ có 3 nghiệm phân biệt

+ Do $\large b\in (-1; 0)\Rightarrow b+1\in (0; 1)\Rightarrow $ Phương trình $\large f(x)=b+1$ có 3 nghiệm phân biệt

+ Do $\large c\in (1; 2)\Rightarrow c+1\in (2; 3)\Rightarrow $ Phương trình $\large f(x)=c+1$ có 1 nghiệm

Vậy phương trình $\large $ có 3 + 3 + 1 =7 nghiệm