Cho hàm số $\Large y=f(x).$ Hàm số $\Large y={f}'(x)$ có đồ thị như hì
MỤC LỤC
Câu hỏi:
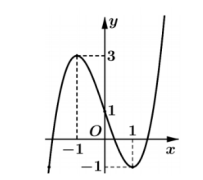
Cho hàm số $\Large y=f(x).$ Hàm số $\Large y={f}'(x)$ có đồ thị như hình bên. Biết $\Large f(-1)=1; f\left(-\dfrac{1}{e}\right)=2.$ Tìm tất cả các giá trị của m để bất phương trình $\Large f(x) < \mathrm{ln} (-x)+m$ nghiệm đúng với mọi $\Large x \in \left(-1; \dfrac{-1}{e}\right).$

Đáp án án đúng là: B
Lời giải chi tiết:
Chọn B
Ta có $\Large f(x) < \mathrm{ln}(-x)+m \Leftrightarrow m > f(x)-\mathrm{ln}(-x).$
Xét hàm số $\Large g(x)=f(x)-\mathrm{ln}(-x)$ trên $\Large \left(-1; -\dfrac{1}{e}\right).$
Có $\Large {g}'(x)={f}'(x)-\dfrac{1}{x}.$
Trên $\Large \left(-1; -\dfrac{1}{e}\right)$ có $\Large {f}'(x) > 0$ và $\Large \dfrac{1}{x} < 0$ nên $\Large {g}'(x) > 0, \forall x \in \left(-1; -\dfrac{1}{e}\right)$
$\Large \Rightarrow$ hàm số $\Large g(x)$ đồng biến trên $\Large \left(-1; -\dfrac{1}{e}\right)$
$\Large \Leftrightarrow m \geq g(x), \forall x \in \left(-1; -\dfrac{1}{e}\right)$
$\Large \Leftrightarrow m \geq g\left(-\dfrac{1}{e}\right)$
$\Large \Leftrightarrow m \geq 3.$
Xem thêm các bài tiếp theo bên dưới
- Cho hình chóp $\Large S.ABC$ có đáy $\Large ABC$ là tam giác đều cạnh
- Cho hàm số $\Large f(x)$ và $\Large g(x)$ liên tục trên đoạn [1; 3] sa
- Cho hình lăng trụ đứng $\Large ABC.A{}'B{}'C{}'$ có đáy là tam giác $\
- Trong không gian $\Large Oxyz$, cho điểm $\Large A(1; -1; -1)$ và mặt
- Trong không gian với hệ tọa độ $\Large Oxyz$, phương trình nào sau đây