Cho hàm số $\Large y =f(x)$ có bảng biến thiên như sau: Giá trị lớn nh

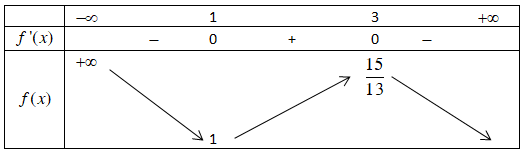
Cho hàm số $\Large y =f(x)$ có bảng biến thiên như sau: 

Giá trị lớn nhất của $\Large m$ để phương trình $\Large e^{2f^3(x)-\frac{13}{2}f^2(x)+7f(x)+\frac{3}{2}}=m$ có nghiệm trên đoạn $\Large [0; 2]$ là: 

 

• A.

  A. $\Large e^4$

   
• B.

  B. $\Large e^3$

   
• C.

  C. $\Large e^{\frac{15}{13}}$

   
• D.

  D. $\Large e^5$

Chọn A

Ta có: $\Large e^{2f^3(x)-\frac{13}{2}f^2(x)+7f(x)+\frac{3}{2}}=m\Leftrightarrow 2f^3(x)-\dfrac{13}{2}f^2(x)+7f(x)+\dfrac{3}{2}=\ln m$

Xét hàm số: $\Large g(x)=2f^3(x)-\dfrac{13}{2}f^2(x)+7f(x)+\dfrac{3}{2}$ có: 

$\Large g'(x)=6f^2(x)f'(x)-13f(x)f'(x)+7f'(x)=f'(x)[6f^2(x)-13f(x)+7]$

Suy ra $\Large g'(x)=0$ $\Large \Leftrightarrow \left[\begin{align}&f'(x)=0\\&6f^2(x)-13f(x)+7=0\\\end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align}&f'(x)=0\\&f(x)=1\\&f(x)=\dfrac{7}{6}\\\end{align}\right.$ $\Large \Leftrightarrow \left[\begin{align}&x=1; x=3\\&x=1; x=x_{1}>3\\&x=x_{2}<1\\\end{align}\right.$

Xét $\Large g(x)$ trên đoạn $\Large [0; 2]$

+) Trong khoảng $\Large (0; 1)$ ta có: $\Large f'(x)<0, f(x)>1; f(x)<\dfrac{7}{6}$ nên $\Large f'(x)(f(x)-1)\left(f(x)-\dfrac{7}{6}\right)>0$ hay $\Large g'(x)>0$

+) Trong khoảng (1; 2) ta có: $\Large f'(x)>0; f(x)>1; f(x)<\dfrac{7}{6}$ nên $\Large f'(x)(f(x)-1)\left(f(x)-\dfrac{7}{6}\right)<0$ hay $\Large g'(x)<0$

Từ đó ta có bảng biến thiên của $\Large g(x)$ như sau: 

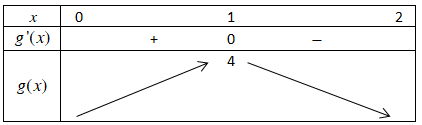
Từ bảng biến thiên ta thấy $\Large \underset{x\in[0; 2]}{\max} g(x)=4$

Vậy yêu cầu bài toán thảo mãn nếu và chỉ nếu $\Large \ln m\leq 4\Leftrightarrow m\leq e^4$ hay giá trị lớn nhất của m là $\Large e^4$