Cho hàm số (C):y=f(x) liên tục trên khoảng (a;b) chứa $\larg
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
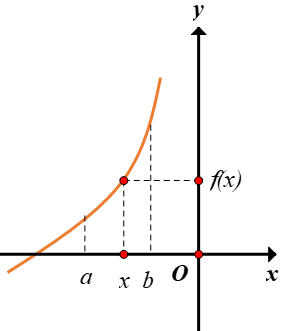
Cho hàm số (C):y=f(x) liên tục trên khoảng (a;b) chứa x0 và các phát biểu sau:
(1) Nếu $\large f(x)
(2) Nếu f(x)≠f(x0),∀x∈(a,b)∖{x0} thì x0 là một điểm cực trị của hàm số (C).
(3) Nếu tồn tại khoảng (e,f)⊂(a,b) sao cho minx0∈(e,f)=f(x0) thì hàm số đạt cực tiểu tại x0.
(4) Nếu f(x)>f(x0),∀x∈(a,b)∖{x0} thì x0 là điểm cực tiểu của hàm số (C).
Có bao nhiêu phát biểu đúng trong các phát biểu đã cho?
Đáp án án đúng là: B
Lời giải chi tiết:
Chọn đáp án B.
Theo định nghĩa cực trị của hàm số : (1);(4) đúng
(2) (3) sai.\ vì
f(x)≠f(x0),∀x∈(a;b)∖{x0}. Tuy nhiên x0 không là điểm cực trị.
Xem thêm các bài tiếp theo bên dưới
- Cho các phát biểu sau: (1) Nếu hàm số đạt cực tiểu tại điểm $\large x_
- Cho hàm số y=f(x) có đồ thị là đường cong trong hình vẽ bên. Hàm số
- Cho hàm số y=f(x) có đạo hàm $\large f^{\prime}(x)=x(x+2)^{2}, \fora
- Cho đồ thị hàm số f′(x) như hình vẽ. Hàm số y=f(x)
- Đường cong trong hình vẽ bên dưới là đồ thị hàm số y=f′(x). Số điểm