Cho hàm số $y=f(x)$ có đạo hàm $\large f^{\prime}(x)=x(x+2)^{2}, \fora

Cho hàm số $y=f(x)$ có đạo hàm $\large f^{\prime}(x)=x(x+2)^{2}, \forall x \in \mathbb{R}$. Số điểm cực trị của hàm số đã cho là .

• A.

  A. 0

• B.

  B. 3

• C.

  C. 2

• D.

  D. 1

Chọn D

Ta có phương trình $\large f^{\prime}(x)=0$ có hai nghiệm x=0 và x=-2 (là nghiệm kép)

Bảng xét dấu:

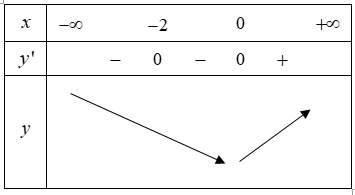
Dựa vào bảng xét dấu suy ra hàm số đã cho có 1 điểm cực trị.

PP nhanh trắc nghiệm

Đề đã cho $\large f^{\prime}(x)$ và để dễ xét dấu $\large f^{\prime}(x)$ thì nhập $\large f^{\prime}(x)$ vào máy tính và chọn 1 số bất kì trong khoảng cần xét thế nào (CALC)