Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình
Lưu về Facebook:

MỤC LỤC
Câu hỏi:
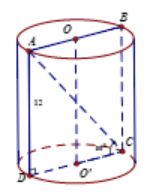
Cắt một khối trụ bởi một mặt phẳng qua trục ta được thiết diện là hình chữ nhật ABCD có AB và CD thuộc hai đáy của khối trụ. Biết AD = 12 và góc ACD bằng $\large 60^{\circ}$. Thể tích của khối trụ là:
Đáp án án đúng là: A
Lời giải chi tiết:
Áp dụng công thức $\large V = \pi R^{2}h$
Với h = 12; $\large R = \dfrac{CD}{2} = \dfrac{ADtan30^{\circ}}{2} = \dfrac{12.\sqrt{3}}{2} = 6\sqrt{3}$
Vậy $\large V = \pi (6\sqrt{3})^{2}.12 = 1296\pi$
Vậy chọn đáp án A.
Xem thêm các bài tiếp theo bên dưới
- Một hình trụ có chu vi của đường tròn đáy là c , chiều cao của hình tr
- Một hình trụ có bán kính đáy bằng R và thiết diện qua trục là hình vuô
- Một khối trụ có thiết diện qua trục là hình vuông, diện tích xung quan
- Gọi $\large S_{xq}$ là diện tích xung quanh của hình nón được sinh ra
- Cho tứ diện đều ABCD có cạnh bằng 3 a . Hình nón ( N ) có đỉnh A và đư