Thể tích của hình hộp chữ nhật
Lý thuyết về Thể tích của hình hộp chữ nhật
1. Đường thẳng vuông góc với mặt phẳng
- Nếu đường thẳng$\left( a \right)$ vuông góc với hai dường thẳng cắt nhau của $mp\left( P \right)$ thì đường thẳng $\left( a \right)$ vuông góc với $mp\left( P \right)$.
- Nếu đường thẳng $\left( a \right)$ vuông góc với $mp\left( P \right)$ tại điểm $I$ thì nó vuông góc với mọi đường thẳng đi qua $I$ và nằm trong $mp\left( P \right)$.
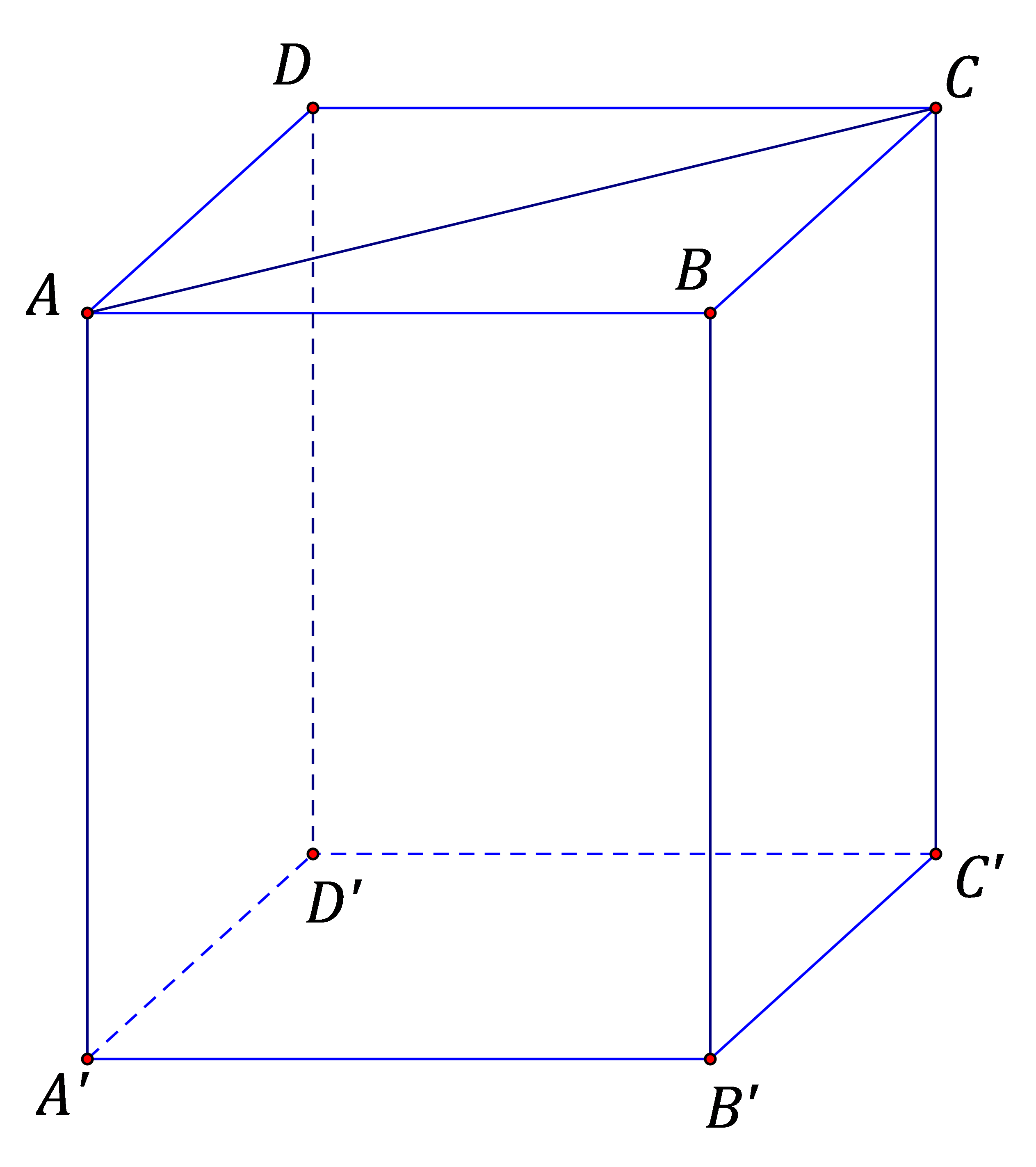
Trên hình 1, $AA'\bot AB,AA'\bot AD$ nên $AA'\bot mp\left( ABCD \right)$; $AA'\bot AC$.
2. Mặt phẳng vuông góc với mặt phẳng
Nếu $mp\left( Q \right)$ chứa một đường thẳng vuông góc với $mp\left( P \right)$ thì vuông góc với $mp\left( P \right)$.
Trên hình 1, \[AA'\bot mp\left( ABCD \right)\] nên $\left( AA'B'B \right)\bot \left( ABCD \right)$
3. Các công thức tính thể tích
Thể tích của hình hộp chữ nhật $V=abc$($a,b,c$ là các kích thước của hình hộp chữ nhật).
Thể tích của hình lập phương: $V={{a}^{3}}$ ($a$ là cạnh của hình lập phương)
Bài tập tự luyện có đáp án
Câu 1: Cho hình lăng hộp chữ nhật $ ABCD.A'B'C'D' $ . 4 điểm nào sau đây không đồng phẳng?
- A
- B
- C
- D

Ta thấy bộ 4 điểm $ A,D,C',A' $ không đồng phẳng.
Các bộ 4 điểm còn lại đều đồng phẳng.
Câu 2: Cho hình hộp chữ nhật $ ABCD.A'B'C'D' $ . Cặp đường thẳng nào sau đây không nằm trong cùng một mặt phẳng?
- A
- B
- C
- D

Dễ thấy $ AB $ và $ A'C' $ không nằm trong cùng 1 mặt phẳng.
Câu 3: Cho hình hộp chữ nhật $ ABCD.A'B'C'D' $ . $ M $ nằm trên $ A'B' $ sao cho $ A'M=\dfrac{1}{2}MB' $ , $ N $ nằm trên $ A'D' $ sao cho $ A'N=\dfrac{1}{3}A'D' $ . Khẳng định đúng trong các khẳng định sau là
- A
- B
- C
- D

$ \dfrac{A'M}{A'B'}=\dfrac{A'N}{A'D}=\dfrac{1}{3}\Rightarrow MN//B'D'//BD\left( talet \right) $ $ \Rightarrow MN//\left( C'BD \right) $
Câu 4: Cho hình hộp chữ nhật $ ABCD.EFGH $ . Các đường thẳng nào vuông góc với mặt phẳng $ EFGH $ . 
- A
- B
- C
- D
Vì $ ABCD.EFGH $ là hình hộp chữ nhật nên $ ABFE,BCGF,CDHG,DAEH $ là hình chữ nhật.
Ta có:
+) $ AE\bot EF $ (Vì $ ABEF $ là hình chữ nhật)
+) $ AE\bot EH $ (Vì $ DAEH $ là hính chữ nhật)
$ \Rightarrow AE\bot mp(EFGH) $
Ta có:
+) $ BF\bot EF $ (Vì $ ABEF $ là hình chữ nhật)
+) $ BF\bot FG $ (Vì $ BCGF $ là hình chữ nhật)
$ \Rightarrow BF\bot mp(EFGH) $ Ta có:
+) $ CG\bot GF $ (Vì $ BCGF $ là hình chữ nhật)
+) $ CG\bot GH $ (Vì $ CDHG $ là hình chữ nhật)
$ \Rightarrow CG\bot mp(EFGH) $
Ta có:
+) $ DH\bot HG $ (Vì $ CDHG $ là hình chữ nhật)
+) $ DH\bot HE $ (Vì $ DAEH $ là hình chữ nhật)
$ \Rightarrow DH\bot mp(EFGH) $
Vậy $ AE,BF,CG,DH $ đều vuông góc với mặt phẳng $ EFGH $ .
Xem thêm các bài tiếp theo bên dưới