Định nghĩa

1. Định nghĩa
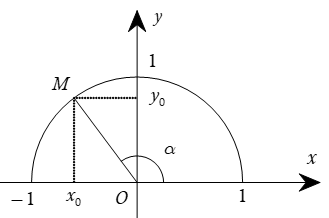
   Với mỗi góc α($0{}^\circ \le \alpha \le 180{}^\circ $) , ta xác định điểm M trên nửa đường tròn đơn vị sao cho $\angle MOx = \alpha $. Giả sử điểm M có tọa độ $\left( {x_0;y_0} \right).$ Khi đó
Tung độ $y_0$ của điểm M gọi là sin của góc α, kí hiệu là sinα. Hoành độ $x_0$ của điểm M gọi là côsin của góc α, kí hiệu là cosα
Tỉ số $\dfrac{y_0}{x_0}$ ( với$x_0 \ne 0$) gọi là tang của góc α, kí hiệu là tanα

Tỉ số $\dfrac{x_0}{y_0}$ ( với $y_0 \ne 0$) gọi là côtang của góc α, kí hiệu là cotα
 

Ví dụ: Tìm các giá trị lượng giác của góc ${{135}^{o}}$
Giải:
  

Ta lấy điểm M  trên đường tròn đơn vị sao cho $\angle MOx = $${{135}^{o}}$. Khi đó hiển nhiên $\angle MOy = $${{45}^{o}}$.

Từ đó suy ra tọa độ của điểm M là $M\left( -\dfrac{\sqrt[{}]{2}}{2};\dfrac{\sqrt[{}]{2}}{2} \right)$
Vậy $\sin{{135}^{o}}=$$\dfrac{\sqrt[{}]{2}}{2}$; $\cos {{135}^{o}}=$$-\dfrac{\sqrt[{}]{2}}{2}$; $\tan{{135}^{o}}=-1$; $\cot {{135}^{o}}=-1$.
Từ đó suy ra :
Nếu hai góc bù nhau thì sin của chúng bằng nhau ,còn côsin, tang và côtang của chúng đối nhau, nghĩa là:
$\begin{align}& \sin \left( {{180}^{o}}-\alpha  \right)=\sin \alpha  \\ & \cos \left( {{180}^{o}}-\alpha  \right)=-\cos \alpha  \\ & \tan \left( {{180}^{o}}-\alpha  \right)=-\tan \alpha \left( \alpha \ne {{90}^{o}} \right) \\ & \tan \left( {{180}^{o}}-\alpha  \right)=-\cot \alpha \left( {{0}^{o}}<\alpha <{{180}^{o}} \right) \\ \end{align}$

2. Giá trị lượng giác của các góc đặc biệt

Trong bảng kí hiệu $''\parallel ''$ để chỉ giá trị lượng giác không xác định.

Chú ý: Từ giá trị lượng giác của các góc đặc biệt đã cho trong bảng và tính chất trên, ta có thể suy ra giá trị lượng giác của một số góc đặc biệt khác như:

$\begin{gathered}  \sin {120^0} = \sin \left( {{{180}^0} - {{60}^0}} \right) = \sin {60^0} = \frac{{\sqrt 3 }}{2} \hfill \\  \cos {135^0} = \cos \left( {{{180}^0} - {{45}^0}} \right) =  - \cos {45^0} =  - \frac{{\sqrt 2 }}{2} \hfill \\ \end{gathered} $

3. Góc giữa hai vectơ

a) Định nghĩa

Cho hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ đều khác vectơ $\overrightarrow{0}.$ Từ một điểm $O$ bất kì ta vẽ $\overrightarrow{OA}=\overrightarrow{a}$ và $\overrightarrow{OB}=\overrightarrow{b}.$ 

Góc $\widehat{AOB}$ với số đo từ ${{0}^{0}}$ đến ${{180}^{0}}$ được gọi là góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}.$ 

Ta kí hiệu góc giữa hai vectơ $\overrightarrow{a}$ và $\overrightarrow{b}$ là $\left( \overrightarrow{a},\overrightarrow{b} \right)$. 

Nếu $\left( \overrightarrow{a},\overrightarrow{b} \right)={{90}^{0}}$ thì ta nói rằng $\overrightarrow{a}$ và $\overrightarrow{b}$ vuông góc với nhau, kí hiệu là $\overrightarrow{a}\bot \overrightarrow{b}$ hoặc $\overrightarrow{b}\bot \overrightarrow{a}.$ 

b) Chú ý. Từ định nghĩa ta có $\left( \overrightarrow{a},\overrightarrow{b} \right)=\left( \overrightarrow{b},\overrightarrow{a} \right).$ 

4. Các hệ thức cơ bản

 $\begin{gathered}  \tan \alpha  = \frac{{\sin \alpha }}{{\cos \alpha }}\left( {\alpha  \ne {{90}^0}} \right) \hfill \\  \cot \alpha  = \frac{{\cos \alpha }}{{\sin \alpha }}\left( {\alpha  \ne {0^0},{{180}^0}} \right) \hfill \\  \tan \alpha .\cot \alpha  = 1 \hfill \\  {\sin ^2}\alpha  + {\cos ^2}\alpha  = 1 \hfill \\  1 + {\tan ^2}\alpha  = \frac{1}{{{{\cos }^2}\alpha }} \hfill \\  1 + {\cot ^2}\alpha  = \frac{1}{{{{\sin }^2}\alpha }} \hfill \\ \end{gathered} $