Nhắc lại về hàm số bậc nhất
Lý thuyết về Nhắc lại về hàm số bậc nhất
Nhắc lại về hàm số bậc nhất
Hàm số bậc nhất là hàm số được cho bằng biểu thức có dạng y=ax+by=ax+b, trong đó a và b là những hằng số với a≠0a≠0.
+TXĐ: D=R
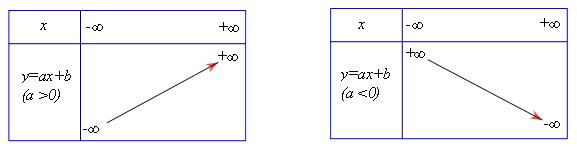
+ Sự biến thiên
- Khi a>0, hàm số y=ax+b đồng biến trên R
- Khi a<0, hàm số y=ax+b nghịch biến trên R
+ Bảng biến thiên:
+ Đồ thị của hàm số y=ax+b(a≠0) là 1 đường thẳng gọi là đường thẳng y=ax+b. Nó có hệ số góc bằng aa và có đặc điểm sau:
- Không song song và không trùng với các trục tọa độ
- Cắt trục tung tại điểm B(0;b) và cắt trục hoành tại điểm A(−b/a;0)
Bài tập tự luyện có đáp án
Câu 1: Số giá trị nguyên âm của m để hàm số y=(2m+3)x−5m+1 đồng biến là
- A
- B
- C
- D
Với 2m+3>0⇔m>−32 thì hàm số đồng biến.
Nên có 1 giá trị nguyên âm thỏa mãn là m=−1.
Câu 2: Tât cả các giá trị của tham số m để hàm số y=m(x+2)−x(2m+1) nghịch biến trên R là
- A
- B
- C
- D
Viết lại y=m(x+2)−x(2m+1)=(−1−m)x+2m .
Hàm số bậc nhất y=ax+b nghịch biến →a<0→−1−m<0⇔m>−1.
Câu 3: Tất cả các giá trị của m thì hàm số y=(m−2018)x−3m−x đồng biến trên R là
- A
- B
- C
- D
Ta có y=(m−2018)x−3m−x=mx−2019x−3m=(m−2019)x−3m .
Khi đó hàm số đồng biến trên R⇔m−2019>0⇔m>2019
Câu 4: Giá trị m để hàm số y=−(m2+1)x+m−4 nghịch biến trên R.
- A
- B
- C
- D
Hàm số bậc nhất y=ax+b nghịch biến ⇔a<0⇔−(m2+1)<0⇔m∈R.
Câu 5: Số giá trị nguyên dương của m để hàm số y=m(x−5)−4x nghịch biến là
- A
- B
- C
- D
Ta có y=m(x−5)−4x=(m−4)x−5m.
Khi đó để hàm số nghịch biến m−4<0⇔m<4.
Câu 6: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2018;2018] để hàm số y=(m−2)x+5m−x đồng biến trên R.
- A
- B
- C
- D
Ta có y=(m−2)x+5m−x=(m−3)x+5m
Hàm số bậc nhất y=ax+b đồng biến ⇔a>0⇔m−3>0⇔m>3.
⇒m∈{4;5;...;2018}. Vậy có 2018−4+1=2015 giá trị nguyên.
Câu 7: Giá trị m để hàm số y=(2m+1)x+m−3 đồng biến trên R.
- A
- B
- C
- D
Hàm số bậc nhất y=ax+b đồng biến ⇔a>0⇔2m+1>0⇔m>−12.
Câu 8: Khẳng định nào về hàm số y=3x+5 là sai:
- A
- B
- C
- D
Đồ thị hàm số y=3x+5 có hệ số góc k=3>0 nên đồng biến trên R .
Vậy khẳng định hàm số nghịch biến trên R sai
Câu 9: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−2017;2017] để hàm số y=(m2−4)x+2m đồng biến trên R.
- A
- B
- C
- D
Hàm số bậc nhất y=ax+b đồng biến →a>0→m2−4>0⇔[m>2m<−2
m∈{−2017;−2016;−2015;...;−3}∪{3;4;5;...;2017}.
Vậy có 2.(2017−3+1)=2.2015=4030 giá trị nguyên của m cần Giá trị.
Câu 10: Số giá trị nguyên nhỏ hơn 10 của m để hàm số y=mx−3−x đồng biến
- A
- B
- C
- D
Ta có y=(m−1)x−3
Với m−1>0⇔m>1 thì hàm số đồng biến
Vậy có 8 giá trị nguyên m<10 thỏa mãn
Câu 11: Số giá trị nguyên âm của m để hàm số y=(2m+5)x−2m+2018 đồng biến
- A
- B
- C
- D
Với 2m+5>0⇔m>−52 thì hàm số đồng biến
Vậy có 2 giá trị nguyên âm thỏa mãn.
Câu 12: Cho hàm số f(x)=(m−2)x−2018 . Khẳng định nào sau đây là đúng
- A
- B
- C
- D
Hàm số f(x)=(m−2)x−2018 đồng biến trên R⇔m−2>0⇔m>2 .
Hàm số f(x)=(m−2)x−2018 nghịch biến trên R⇔m−2<0⇔m<2 .
Câu 13: Với những giá trị nào của m thì hàm số f(x)=(m+1)x+2 đồng biến?
- A
- B
- C
- D
Hàm số f(x)=(m+1)x+2 đồng biến ⇔m+1>0⇔m>−1 .
Xem thêm các bài tiếp theo bên dưới