Định lí đảo và hệ quả của định lí Ta - let
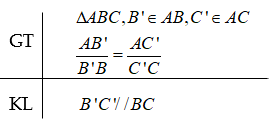
Lý thuyết về Định lí đảo và hệ quả của định lí Ta - let
1. Định lí đảo của định lí Talet
Nếu một đường thẳng cắt hai cạnh một tam giác và định ra trên hai cạnh ấy những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Ví dụ: Cho hình vẽ bên dưới. Hãy chỉ ra các cặp cạnh song song với nhau
Ta có
ADBD=36=510=AEEC⇒DE//BCCEAE=105=147=CFBF⇒EF//AB
2. Hệ quả của định lí Talet
Nếu một đường thẳng cắt hai cạnh còn lại của một của một tam giác và song song với các cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh còn lại của tam giác đã cho.
*Chú ý: Hệ quả trên vẫn đúng cho trường hợp đường thẳng a song song với một cạnh của tam giác và cắt phần còn lại kéo dài của hai cạnh còn lại.
Bài tập tự luyện có đáp án
Câu 1: Cho tam giác ABC vuông tại A,MN//BC,BC=12cm,AM=8cm,AN=6cm. Diện tích tam giác ABC bằng
- A
- B
- C
- D

Áp dụng Pi-ta-go trong tam giác vuông AMN ta có MN=√AM2+AN2=√82+62=10
Ta có MN//BC⇒AMAB=ANAC=MNAM
⇔8AB=6AC=1012⇒AB=8.1210=485;AC=6.1210=365
Khi đó diện tích tam giác ABC bằng: SABC=12AB.AC=12.485.365=86425
Câu 2: Cho tam giác ABC có BC=a . Trên cạnh AB lấy các điểm D và E sao cho AD=DE=EB . Từ D,E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M và N. Tổng độ dài 2 đoạn thẳng DM và EN theo a bằng
- A
- B
- C
- D

Ta có: AD=DE=EB=13AB(gt)(1) ⇒AE=AD+DE=23AB(2)
Trong ΔABC , ta có: DM//BC(gt)
Nên ADAB=DMBC⇔ADAB=DMa(3)
Từ (1);(3) ta có 13=DMa⇒DM=a3
Trong ΔABC , ta có: EN//BC(gt) ⇒AEAB=ENBC⇒AEAB=ENa(4)
Từ (2);(4) suy ra: 23=ENa⇒EN=2a3
⇒DM+EN=a3+2a3=a
Câu 3: Cho biết MN//BC,AB=14cm,MN=13cm,AM=12cm,AC=16cm . Khi đó x+y bằng


- A
- B
- C
- D
MN//BC⇒MAAC=NAAB=MNBC⇔1216=y14=13x⇒y=12.1416=212;x=13.1612=523
⇒x+y=212+523=1676cm
Câu 4: Một đường thẳng đi qua đỉnh A của hình bình hành ABCD cắt BD, BC, DC theo thứ tự ở E, K, G. Khi đó ta có đẳng thức
- A
- B
- C
- D

Vì BK//AD và AB//DG nên theo hệ quả định lý Ta-lét ta có:
EKAE=EBED=AEEG⇒AE2=EK.EG
Câu 5: Cho AB//CD,M∈AB,N∈CD, điểm O∈MN,MN=5cm,OB=1,5cm,OD=6cm . Độ dài đoạn OM bằng
- A
- B
- C
- D

Ta có MB//DN⇒OBOD=MOON=1,56=14⇒NO=4MO
Mà MN=MO+ON=5cm⇒OM+4OM=5cm⇒OM=1cm
⇒ON=4cm
Câu 6: Cho △ABC đường phân giác trong AD . Biết ˆA=1200 thì 1AB+1AC
- A
- B
- C
- D

Qua C kẻ CF//AD,F∈AB , ta có: ˆF=^DAB=600 (1)
^FCA=^CAD=600 (2)
Từ (1) và (2) suy ra △AFC đều ⇒AF=FC=AC⇒BF=AB+AF=AB+AC
Áp dụng hệ quả định lý Ta-lét vào △BFC,AD//FC:
ADFC=BABF hay ADAC=ABAB+AC ⇒AD =AC.ABAB+AC
⇒1AD=AB+ACAB.AC=1AB+1AC
Xem thêm các bài tiếp theo bên dưới