Các bước lập phương trình dao động dao động điều hoà
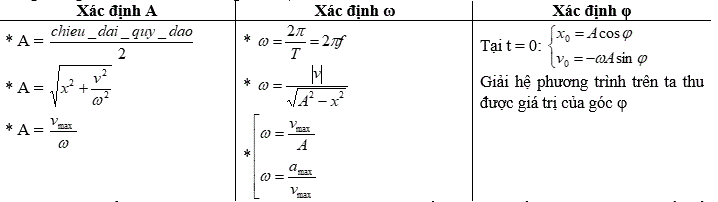
Lý thuyết về Các bước lập phương trình dao động dao động điều hoà
Giả sử cần lập phương trình dao động điều hòa có dạng x = Acos(ωt + φ). Để viết phương trình dao động chúng ta cần tìm ba đại lượng A, ω, φ.
Chú ý:
* Với thể loại bài toán lập phương trình thì chúng ta cần xác định gốc thời gian (t = 0), nếu đề bài không yêu cầu thì để cho đơn giản hóa bài toán chúng ta chọn gốc thời gian lúc vật qua vị trí cân bằng theo chiều dương.
* Khi thả nhẹ để vật dao động điều hòa thì ta hiểu là vận tốc ban đầu vo = 0, còn nếu cho vận tốc ban đầu vo 0 thì chúng ta áp dụng hệ thức liên hệ để tìm các thông số khác.
VD: Một vật dao động điều hòa với biên độ A =4cm và T = 2s. Chọn gốc thời gian là lúc vật qua VTCB theo chiều dương của quỹ đạo. Phương trình dao động của vật là :
HD : w = 2πf = π. và A = 4cm
t =0 : x0 = 0, v0 > 0 : {0=cosφv0=−Aωsinφ>0 nên {φ=±π2sinφ<0 chọn φ = - π/2 suy ra x = 4cos(2πt - π/2)cm.
Bài tập tự luyện có đáp án
Câu 1: Phương trình biểu diễn một vật dao động điều hòa với biên độ 12cm, có tần số góc πrad/s và có pha ban đầu bằng π4 là:
- A
- B
- C
- D
Vật dao động điều hòa có phương trình: x=Acos(ωt+φ)(cm)
Trong đó A là biên độ dao động, ω là tần số góc và φ là pha ban đầu
Mà A=12cm,φ=π4,ω=πrad/s nên phương trình dao động có dạng: x=12cos(πt+π4)(cm)
Câu 2: Một chất điểm dao động điều hòa trên trục Ox có phương trình x=4sin(2πt+π6)(cm) phương trình biểu diễn gia tốc của chất điểm khi đó có dạng
- A
- B
- C
- D
Phương trình dao động của vật: x=4sin(2πt+π6)(cm)
Phương trình biểu diễn gia tốc của chất điểm khi đó là: a=x″=−w2x=−16π2sin(2πt+π6)(cm/s)
Câu 3: Phương trình li độ của chất điểm dao động điều hòa có dạng x=Asin(ωt)(cm) kết luận nào sau đây là đúng?
- A
- B
- C
- D
Ta có phương trình dao động của chất điểm: x=Asin(ωt)(cm)
Tại thời điểm t=0 thì x=A.sin0=0 và vận tốc v=Aω.cos0 = Aω0
Tại thời điểm t = 0 vật đi qua vị trí cân bằng theo chiều dương
Câu 4: Một vật dao động điều hòa có phương trình vận tốc v=4πcos2πt(cm/s) . Gốc tọa độ tại vị trí cân bằng, mốc thời gian được chọn vào lúc vật có li độ và vân tốc là:
- A
- B
- C
- D
Phương trình biểu diễn một vật dao động điều hòa có dạng: x=Acos(ωt+φ)
⇒v=−Aωsin(ωt+φ)=Aωcos(ωt+φ+π2)
Đối chiếu phương trình bài cho ta được: {Aω=4πφ+π2=0 ⇒{A=2cmφ=−π2
Tại thời điểm t = 0 ta có ⇒{x0=2cos(2π.0+π2)=0v0=4πcos(2π.0)=4π
Gốc thời gian được chọn khi vật ở x=0,v=4π
Câu 5: Một chất điểm dao động điều hòa trên trục Ox có phương trình x=Acos(ωt+φ)(cm) phương trình biểu diễn gia tốc của chất điểm khi đó có dạng:
- A
- B
- C
- D
Một chất điểm dao động điều hòa trên trục Ox có phương trình x=Acos(ωt+φ)(cm)
Phương trình biểu diễn gia tốc tốc chất điểm khi đó là: a=x″=−Aω2cos(ωt+φ)(cm/s2)
Câu 6: Phương trình biểu diễn vận tốc của một vật dao động điều hòa có dạng v=ωAcosωt(cm/s) . Phương trình biểu diễn li độ của chất điểm khi đó
- A
- B
- C
- D
Vì v=x′ nên x=∫v=∫ωAcos(ωt)dt = A.sin(ωt)
Câu 7: Một vật dao động điều hòa với biên độ A, tần số góc ω . Gia tốc của chất điểm ở vị trí biên có độ lớn bằng bao nhiêu?
- A
- B
- C
- D
Một chất điểm dao động điều hòa trên trục Ox có phương trình x=Acos(ωt+φ)(cm)
Phương trình biểu diễn gia tốc khi đó là: a=x″=−Aω2cos(ωt+φ)(cm/s2)=-ω2x
Khi vật ở vị trí biên thì x=±A gia tốc chất điểm khi đó là: a=±ω2A(cm/s2)
Độ lớn của gia tốc ω2A
Câu 8: Phương trình biểu diễn một vật dao động điều hòa với biên độ 5cm, có tần số góc ω và có pha ban đầu bằng 0 là:
- A
- B
- C
- D
Vật dao động điều hòa có phương trình: x=Acos(ωt+φ)(cm)
Trong đó A là biên độ dao động, ω là tần số góc và φ là pha ban đầu
Mà A=5cm,φ=0 nên phương trình dao động có dạng: x=5cos(ωt)(cm)
Câu 9: Một chất điểm dao động điều hòa trên trục Ox với tần số góc là 10rad/s, pha ban đầu của chất điểm là π6 biên độ dao động của vật là 2cm. Phương trình biểu diễn li độ của chất điểm
- A
- B
- C
- D
Vật dao động điều hòa có phương trình: x=Acos(ωt+φ)(cm)
Trong đó A là biên độ dao động, ω là tần số góc và φ là pha ban đầu
Mà A=2cm,φ=π6,ω=10rad/s nên phương trình dao động có dạng: x=2cos(10t+π6)(cm)
Câu 10: Một chất điểm dao động điều hòa trên trục Ox có phương trình x=6sin(2πt)(cm) phương trình biểu diễn vận tốc của chất điểm khi đó có dạng:
- A
- B
- C
- D
Cách 1: Phương trình dao động của vật: x=6sin(2πt)(cm)
Phương trình biểu diễn vận tốc khi đó là: v=x′=12πcos(2πt)(cm/s)
Cách 2:
Phương trình dao động của vật: x=6sin(2πt)=6cos(2πt−π2)
Phương trình biểu diễn vận tốc khi đó là:
v=x′=−6.2π.sin(2πt−π2)=−12πsin(2πt−π2)=12πsin(−12πt+π2)=12πcos(12πt)
Câu 11: Một chất điểm dao động điều hòa trên trục Ox có phương trình x=Acos(ωt+φ)(cm) phương trình biểu diễn vận tốc của chất điểm khi đó có dạng:
- A
- B
- C
- D
Một chất điểm dao động điều hòa trên trục Ox có phương trình x=Acos(ωt+φ)(cm)
Phương trình biểu diễn vận tốc khi đó là: v=x′=−Aωsin(ωt+φ)(cm/s)