Quãng đường lớn nhất
Lý thuyết về Quãng đường lớn nhất
t=nT+T/2+$\Delta t$
Trong nT vật đi được quãng đường là 4nA, Trong T/2 vật luôn đi được quãng đường là 2A.
Trong khoảng thời gian $\Delta t$ vật quét được góc: $\Delta \varphi =\omega .\Delta t$
Vật đi được quãng đường lớn nhất trong một khoảng thời gian cho trước thì vật phải có tốc độ lớn nhất .Mà tốc độ lớn nhất của vật ở VTCB nên vật muốn có quãng đường lớn nhất vật phải đi quanh VTCB.
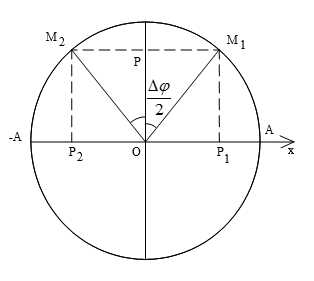
Quãng đường lớn nhất khi vật đi từ M1 đến M2 đối xứng qua trục sin
$\begin{align} & {{M}_{1}}{{M}_{2}}={{P}_{1}}{{P}_{2}}=2O{{P}_{1}} \\ & O{{P}_{1}}\text{=A}\sin \frac{\Delta \varphi }{2} \\ \end{align}$
${{M}_{1}}{{M}_{2}}=$${{S}_{M\text{ax}}}=2\text{A}\sin \dfrac{\Delta \varphi }{2}$$\left( \Delta \varphi \le \frac{\pi }{2} \right)$
Bài tập tự luyện có đáp án
Câu 1: Một vật dao động điều hòa với biên độ A và chu kỳ T. Trong khoảng thời gian $\Delta t = \frac{T}{4}$, quãng đường lớn nhất ($S_{max}$) mà vật đi được là
- A
- B
- C
- D
Trong khoảng thời gian$ ∆t = T/4$, quãng đường lớn nhất ($S_{max}$) mà vật đi được là
${{S}_{m}}_{\text{ax}}=2A\sin \dfrac{\dfrac{2\pi }{T}.t}{2}=2A\sin \dfrac{\dfrac{2\pi }{T}.\dfrac{T}{4}}{2}=A\sqrt{2}$