Tìm quỹ tích điểm qua phép vị tự
Lưu về Facebook:
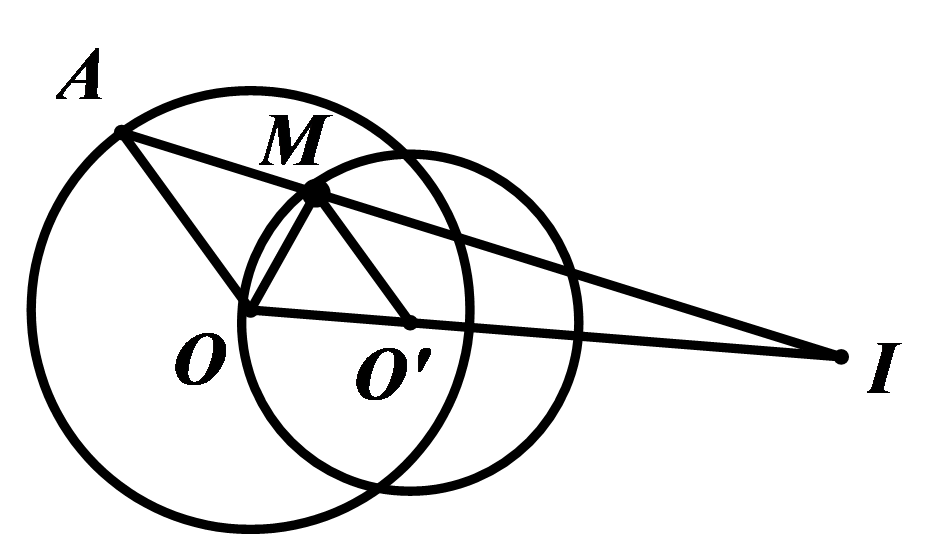
Lý thuyết về Tìm quỹ tích điểm qua phép vị tự
Phương pháp
Để tìm tập hợp điểm M ta có thể quy về tìm tập hợp điểm N và tìm một phép vị tự V(I;k) nào đó sao cho V(I;k)(N)=M suy ra quỹ tích điểm M là ảnh của quỹ tích N qua V(I;k).
Ví dụ: Cho đường tròn (O;R) và một điểm I nằm ngoài đường tròn sao cho OI=3R, A là một điểm thay đổi trên đường tròn (O;R). Phân giác trong góc ^IOA cắt IA tại điểm M. Tìm tập hợp điểm M khi A di động trên (O;R).
Lời giải:
Theo tính chất đường phân giác ta có MIMA=OIOA=3RR=3
⇒IM=34IA
⇒→IM=34→IA
⇒V(I;34)(A)=M , mà A thuộc đường tròn (O;R) nên M thuộc (O′;34R) ảnh của (O;R) qua V(I;34). Vậy tập hợp điểm M là (O′;34R) ảnh của (O;R) qua V(I;34).
Bài tập tự luyện có đáp án
Câu 1: Cho phép vị tự M′=V(O,k)(M),N′=V(O,k)(N) . Chọn khẳng định sai:
- A
- B
- C
- D
Khẳng định “ M′N′=k.MN” là sai vì M′N′=|k|.MN