Tiệm cận của hàm phân thức b1/b1
Lý thuyết về Tiệm cận của hàm phân thức b1/b1
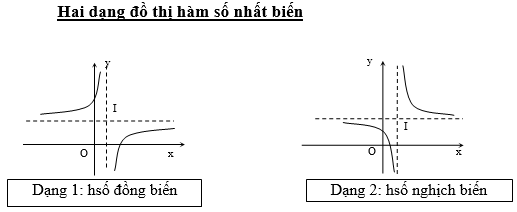
Đồ thị hàm phân thức bậc nhất trên bậc nhất dạng y=ax+bcx+d(c≠0;ad−bc≠0) luôn có hai tiệm cận:
- Tiệm cận đứng x=−dc
- Tiệm cận ngang y=ac
Giao điểm I(−dc;ac) cùa hai đường tiệm cận trên chính là tâm đối xứng của đồ thị hàm số
Bài tập tự luyện có đáp án
Câu 1: Cho đồ thị hai hàm số y=1x+1(C1), y=2x+1(C2). Khẳng định nào sau đây là đúng
- A
- B
- C
- D
(C1);(C2) có tử là hằng số và chung mẫu (x+1) nên ta có x=−1 làm tiệm cận đứng
và có tiệm cận ngang y=0
Suy ra, (C1),(C2) có chung tiệm cận
Câu 2: Cho hàm số y=3x−22x+3 , chọn khẳng định đúng trong các khẳng định sau:
- A
- B
- C
- D
Đồ thị hàm số có tiệm cận đứng là x=−32 , tiệm cận ngang là y=32⇒ giao điểm của hai đường tiệm cận là (−32;32)∈ góc phần tư thứ hai
Câu 3: Đồ thị hàm số nào sau đây nhận đường thẳng y=1 làm tiệm cận ngang?
- A
- B
- C
- D
Vì y=x2−1 và y=x3−3x là hàm đa thức nên loại.
Mà limx→+∞(1−2x−1)=1 nên chọn.
Câu 4: Số đường tiệm cận (nếu có) của đồ thị hàm số y=1−2x+3 là
- A
- B
- C
- D
Hàm số có hai tiệm cận là x=32 và y=0 .
Câu 5: Đồ thị hàm số y=xx−m luôn có tiệm cận đứng khi ?
- A
- B
- C
- D
Đồ thị hàm số y=xx−m luôn có tiệm cận đứng ⇔m≠0.
Câu 6: Tiệm cận đứng của đồ thị hàm số y=1x là
- A
- B
- C
- D
Ta có limx→0+1x=+∞⇒x=0 là tiệm cận đứng hay đồ thị hàm số nhận trục Oy làm tiệm cận đứng.
Câu 7: Đường thẳng y=1 là tiệm cận ngang của đồ thị hàm số nào sau đây?
- A
- B
- C
- D
Nhìn vào các phương án, ta chọn được đáp án là y=1−x2−x.
Câu 8: Đồ thị hàm số nào sau đây không có tiệm cận?
- A
- B
- C
- D
Hàm số y=−x3+2x−1 là hàm bậc 3 nên không có tiệm cận.
Câu 9:  Cho đồ thị hàm số y=f(x) như hình bên. Khẳng định nào sau đây là sai?
Cho đồ thị hàm số y=f(x) như hình bên. Khẳng định nào sau đây là sai?
 Cho đồ thị hàm số y=f(x) như hình bên. Khẳng định nào sau đây là sai?
Cho đồ thị hàm số y=f(x) như hình bên. Khẳng định nào sau đây là sai?- A
- B
- C
- D
Từ đồ thị hàm số ta thấy hàm số luôn đồng biến trên các khoảng của tập xác định nên khẳng định “Hàm số luôn nghịch biến trên các khoảng của tập xác định” là sai.