Phương trình chính tắc elip
Lý thuyết về Phương trình chính tắc elip
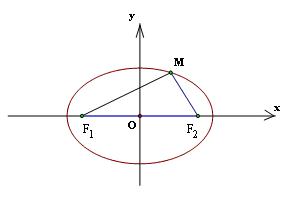
Cho elip $(E)$ như trong định nghĩa. Ta chọn hệ trục tọa độ $Oxy$ có gốc là trung điểm đoạn thẳng $F1F2$. Trục $Oy$ là trung trực của $F1F2$ và $F2$ nằm trên tia $Ox$
Các đoạn thẳng $MF1,MF2$ được gọi là bán kính qua tiêu của điểm $M$. Bây giờ ta lập phương trình của elip $(E)$ đối với hệ trục tọa độ đã chọn như trên.
Ta có:
$M{{F}_{1}}=a+\dfrac{cx}{a}=\sqrt[{}]{{{\left( x+c \right)}^{2}}+{{y}^{2}}}$ hay${{\left( a+\dfrac{cx}{a} \right)}^{2}}={{\left( x+c \right)}^{2}}+{{y}^{2}}$
Rút gọn đẳng thức trên ta được$\left( 1-\dfrac{{{c}^{2}}}{{{a}^{2}}} \right){{x}^{2}}+{{y}^{2}}={{a}^{2}}-{{c}^{2}}$, hay $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{a}^{2}}-{{c}^{2}}}=1$ vì ${{a}^{2}}-{{c}^{2}}>0$ nên ta có thể đặt ${{a}^{2}}-{{c}^{2}}={{b}^{2}}$ (với b > 0) và được
$\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ $(a>b>0) $ (1)
Phương trình (1) gọi là phương trình chính tắc của elip đã cho.
Ví dụ : Viết phương trình chính tắc của elip đi qua hai điểm M(0;1) và
$N\left( 1;\dfrac{\sqrt[{}]{3}}{2} \right)$ . Xác định toạ độ các tiêu điểm của elip đó
Giải : Phương trình chính tắc của elip có dạng $\dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ $(a>b>0) $
Elip đi qua $M ( 0;1)$ nên $\dfrac{1}{{{b}^{2}}}=1$hay${{b}^{2}}=1$. Elip đó đi qua$N\left( 1;\dfrac{\sqrt[{}]{3}}{2} \right)$nên $\dfrac{1}{{{a}^{2}}}+\dfrac{3}{4{{b}^{2}}}=1$
Suy ra ${{a}^{2}}=4$. Vậy elip cần tìm cho phương trình chính là $\dfrac{{{x}^{2}}}{4}+\dfrac{{{y}^{2}}}{1}=1$
Ta có ${{c}^{2}}={{a}^{2}}-{{b}^{2}}=4-1=3$. Vậy toạ độ các tiêu điểm của elip đó là
$F1\left( -\sqrt[{}]{3};0 \right)$ và $F2\left( \sqrt[{}]{3};0 \right)$
Bài tập tự luyện có đáp án
Câu 1: Phương trình chính tắc của elip $ 4{{x}^{2}}+9{{y}^{2}}=36 $ là :
- A
- B
- C
- D
Ta có: $ 4{{x}^{2}}+9{{y}^{2}}=36\Leftrightarrow \dfrac{1}{36}\left( 4{{x}^{2}}+9{{y}^{2}} \right)=1\Leftrightarrow \dfrac{{{x}^{2}}}{9}+\dfrac{{{y}^{2}}}{4}=1 $
Câu 2: Phương trình chính tắc của Elíp có độ dài trục lớn bằng $ 8 $ , độ dài trục bé bằng $ 6 $ là:
- A
- B
- C
- D
Độ dài trục lớn bằng $ 2\text{a}=8\Leftrightarrow a=4 $ .
Độ dài trục bé bằng $ 2b=6\Leftrightarrow b=3 $ .
Phương trình chính tắc của Elíp : $ \dfrac{{{x}^{2}}}{16}+\dfrac{{{y}^{2}}}{9}=1 $ .
Câu 3: Phương trình chính tắc của elip $ 4{{x}^{2}}+9{{y}^{2}}=1 $ là
- A
- B
- C
- D
Ta có: $ 4{{x}^{2}}+9{{y}^{2}}=1\Leftrightarrow \dfrac{{{x}^{2}}}{\dfrac{1}{4}}+\dfrac{{{y}^{2}}}{\dfrac{1}{9}}=1 $
Câu 4: Phương trình nào sau đây là phương trình chính tắc của elip
- A
- B
- C
- D
Phương trình chính tắc của elip là : $ \dfrac{{{x}^{2}}}{{{a}^{2}}}+\dfrac{{{y}^{2}}}{{{b}^{2}}}=1 $
Câu 5: Phương trình chính tắc của elip $ {{x}^{2}}+4{{y}^{2}}=1 $ là :
- A
- B
- C
- D
Ta có: $ {{x}^{2}}+4{{y}^{2}}=1\Leftrightarrow \dfrac{{{x}^{2}}}{1}+\dfrac{{{y}^{2}}}{\dfrac{1}{4}}=1 $
Xem thêm các bài tiếp theo bên dưới