Nhắc lại và bổ sung các khái niệm về hàm số
Lý thuyết về Nhắc lại và bổ sung các khái niệm về hàm số
1. Định nghĩa hàm số
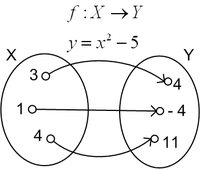
Cho $X,Y$ là hai tập hợp số, hàm số $f$ xác định trên $X$, nhận giá trị trong $Y$ là một quy tắc cho tương ứng mỗi số $x$ thuộc $X$ với một số $y$ duy nhất thuộc $Y$
Ví dụ: $y=x^2-5$
– Khi $x$ thay đổi mà $y$ luôn nhận một giá trị không đổi thì $y$ được gọi là một hàm hằng.
2. Đồ thị của hàm số
Tập hợp các điểm biểu diễn các cặp giá trị tương ứng $(x; f(x))$ trên mặt phẳng tọa độ được gọi là đồ thị của hàm số $y = f(x).$
3. Hàm số đồng biến, hàm số nghich biến
Cho hàm số $y = f(x)$ xác định với mọi giá trị của x thuộc tập số thực $R.$ Với 
tùy ý thuộc $R:$
a) Nếu $x_1< span=""> mà $f\left( {{x_1}} \right) < f\left( {{x_2}} \right)$ thì hàm số được gọi là hàm đồng biến.b) Nếu $x_1< span=""> mà $f\left( {{x_1}} \right) > f\left( {{x_2}} \right)$ thì hàm số được gọi là hàm nghịch biến.$<><>
Bài tập tự luyện có đáp án
Câu 1: Cho hàm số $ y=\left( 3m-2 \right)x+5m $ . Tìm m để hàm số nhận giá trị là 2 khi $ x=-1 $
- A
- B
- C
- D
Thay $ x=-1;y=2 $ ta có:
$ 2=2-3m+5m\Leftrightarrow m=0 $
Câu 2: Cho hàm số $ f\left( x \right)=-\dfrac{1}{4}x $ có đồ thị $ \left( C \right) $ và các điểm $ M\left( 0;4 \right),P\left( 4;-1 \right),Q\left( -4;1 \right),A\left( 8;-2 \right),O\left( 0;0 \right) $ có bao nhiêu điểm trong số các điểm trên thuộc đồ thị hàm
- A
- B
- C
- D
Lần lượt thay tọa độ các điểm $ M,O,P,Q,A $ ta được các điểm $ O,P,Q,A $ thỏa mãn đồ thị hàm số $ f\left( x \right)=-\dfrac{1}{4}x $
Câu 3: Cho hàm số $ y=\left( {{m}^{2}}+m+1 \right)x-2 $ . Tìm m để hàm số đồng biến
- A
- B
- C
- D
Hàm số luôn luôn đồng biến vì $ {{m}^{2}}+m+1={{\left( m+\dfrac{1}{2} \right)}^{2}}+\dfrac{3}{4} > 0 $ với mọi m
Câu 4: Tìm giá trị lớn nhất của $A = x + \sqrt{2-x} $
- A
- B
- C
- D
Điều kiện $x ≤ 2$. Đặt $ \sqrt{2-x} = y$ ≥ 0, ta có: \[{y^2} = 2 - x\]
$ a=2-{{y}^{2}}+y=-{{\left( y-\dfrac{1}{2} \right)}^{2}}+\dfrac{9}{4}\le \dfrac{9}{4}\,\,\,\\\Rightarrow \,\,\,m\text{ax}\,\text{A}\,\text{=}\,\,\dfrac{\text{9}}{\text{4}}\,\,\Leftrightarrow y=\dfrac{1}{2}\,\,\Leftrightarrow \,\,x=\dfrac{7}{4} $
Xem thêm các bài tiếp theo bên dưới