Định nghĩa hình chóp đều
Lý thuyết về Định nghĩa hình chóp đều
Hình chóp đều là hình chóp thoả 2 điều kiện sau:
- Đáy là đa giác đều (tam giác đều, hình vuông, ...)
- Chân đường cao của hình chóp là tâm của đáy
Từ định nghĩa suy ra hình chóp đều có các cạnh bên bằng nhau.
Ví dụ:
1. Hình chóp đều $S.ABCD$ có: $ABCD$ là hình vuông, H là giao điểm của hai đường chéo thì $𝑆𝐻\bot (𝐴𝐵𝐶𝐷)$.
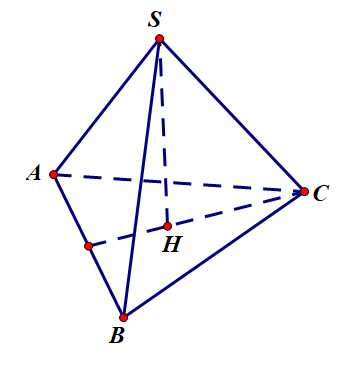
2. Hình chóp đều $S.ABC$ (tứ diện đều) có: $ABC$ là tam giác đều, $H$ là giao điểm của 3 đường trung tuyến thì $SH\bot (ABC)$.
Bài tập tự luyện có đáp án
Câu 1: Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích V của khối chóp S.ABC.
Cho khối chóp tam giác đều S.ABC có cạnh đáy bằng a và cạnh bên bằng 2a. Tính thể tích V của khối chóp S.ABC.
- A
- B
- C
- D
Gọi $H$ là trọng tâm tam giác $ABC$ Khi đó $SH$ là chiều cao của khối chóp.
Ta có $CH=\dfrac{a\sqrt[{}]{3}}{3},SH=\sqrt[{}]{SC^2-HC^2}=\sqrt{4{{a}^{2}}-\dfrac{{{a}^{2}}}{3}}=a\sqrt{\dfrac{11}{3}}$
$\Rightarrow V=\dfrac{1}{3}{{S}_{ABC}}.SH=\dfrac{1}{3}.\dfrac{{{a}^{2}}\sqrt{3}}{4}.a\sqrt{\dfrac{11}{3}}=\dfrac{{{a}^{3}}\sqrt{11}}{12}$

Câu 2: Khẳng định nào sau đây là đúng
- A
- B
- C
- D
Xem thêm các bài tiếp theo bên dưới