Chuyển động tròn đều
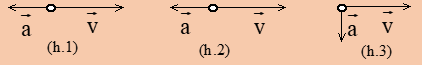
Lý thuyết về Chuyển động tròn đều
Chuyển động tròn đều là chuyển động có quỹ đạo tròn và có tốc độ trung bình trên mọi cung tròn là như nhau.
- Công thức chu kì $T=\dfrac{2.\pi }{\omega }\left( s \right)$
- Công thức tần số: $f=\dfrac{1}{T}=\dfrac{\omega }{2.\pi }\left( H\text{z} \right)$
- Công thức gia tốc hướng tâm:${{a}_{ht}}=\dfrac{{{v}^{2}}}{r}=r.{{\omega }^{2}}\left( m/{{s}^{2}} \right)$
$\omega $ là tốc độ góc của chuyển động tròn đều là một đại lượng không đổi.
Đơn vị tốc độ góc là rad/s.
Bài tập tự luyện có đáp án
Câu 1: Chọn phát biểu sai về chuyển động tròn đều
- A
- B
- C
- D
$ v=\omega .r=\dfrac{2\pi .r}{T} $ , với r là hằng số thì v tỉ lệ nghịch với T.
Câu 2: Chuyển động của vật nào dưới đây là chuyển động tròn đều?
- A
- B
- C
- D
Chuyển động của điểm đầu cánh quạt khi quay ổn định là chuyển động tròn đều.
Câu 3: Chọn phát biểu sai về một chuyển động tròn đều bán kính r
- A
- B
- C
- D
$ T=\dfrac{2\pi }{\omega } $ , chu kì T tỉ lệ nghịch với tốc độ góc.
Câu 4: Chọn phát biểu đúng về các chuyển động tròn
- A
- B
- C
- D
Thành phần gia tốc dọc tiếp tuyến quỹ đạo tròn quyết định sự không đều của chuyển động tròn. Thành phần đó cùng chiều với véctơ vận tốc thì chuyển động đó là tròn nhanh dần và ngược lại
Câu 5: Chọn câu trả lời sai. Chuyển động của các vật dưới đây là chuyển động tròn đều.
Chuyển động của các vật dưới đây là chuyển động tròn đều.
- A
- B
- C
- D
Chuyển động tròn đều là chuyển động của cái đầu van xe đạp đối với người trên xe, xe chạy đều
Câu 6: Chọn phát biểu sai. Trong chuyển động tròn đều,
- A
- B
- C
- D
Gia tốc hướng tâm đặc trưng cho sự thay đổi về hướng của vectơ vận tốc.
Câu 7: Phát biểu nào sau đây là sai khi nói về chuyển động tròn đều.
- A
- B
- C
- D
Công thức tính quãng đường trong chuyển động tròn đều. $ S=\omega .t.R $
Câu 8: Biểu thức nào sau đây đúng với biểu thức của gia tốc hướng tâm?
- A
- B
- C
- D
Biểu thức của gia tốc hướng tâm \[ {{a}_{ht}}=\dfrac{{{v}^{2}}}{r}={{\omega }^{2}}r \].
Câu 9: Trong chuyển động tròn đều vectơ vận tốc có.
- A
- B
- C
- D
Trong chuyển động tròn đều vectơ vận tốc có độ lớn không đổi và có phương luôn trùng với tiếp tuyến của quỹ đạo tại mỗi điểm
Câu 10: Chu kỳ của kim giờ là
- A
- B
- C
- D
Kim giờ quay một vòng hết 12 tiếng.
Câu 11: Trong chuyển động tròn đều của một chất điểm, gia tốc tức thời.
- A
- B
- C
- D
Trong chuyển động tròn đều của một chất điểm, gia tốc tức thời hướng vào tâm của quĩ đạo.
Câu 12: Chu kỳ của kim phút là
- A
- B
- C
- D
Kim phút quay một vòng hết 60 phút.
Câu 13: Chọn phát biểu đúng.
- A
- B
- C
- D
Trong chuyển động tròn đều phương của vector vận tốc tức thời vuông góc với bán kính của quỹ đạo tại mọi điểm
Câu 14: Chọn phát biểu sai trong các câu sau khi nói về một đĩa tròn quay đều quanh tâm của nó.
- A
- B
- C
- D
Tất cả các điểm trên đĩa chuyển động tròn đều với tốc độ góc như nhau
Câu 15: Có ba chuyển động với các vectơ vận tốc và gia tốc như sau. Chuyển động nào là chuyển động tròn đều?


- A
- B
- C
- D
Trong chuyển động tròn đều, vectơ gia tốc luôn vuông góc với vectơ gia tốc
Câu 16: Chọn biểu thức đúng về độ lớn của gia tốc hướng tâm?
- A
- B
- C
- D
Biểu thức đúng là: $ {{a}_{ht}}={{\omega }^{2}}r $.
Câu 17: Chu kỳ của kim giây là
- A
- B
- C
- D
Kim giây quay một vòng hết 1 phút.
Câu 18: Chọn phát biểu sai. Hai chất điểm chuyển động tròn đều có cùng chu kỳ.
- A
- B
- C
- D
Tốc độ góc là như nhau.
Câu 19: Các công thức liên hệ giữa tốc độ góc \[\omega \] với chu kỳ T và giữa tốc độ góc \[\omega \] với tần số f trong chuyển động tròn đều là
- A
- B
- C
- D
Trong chuyển động tròn đều $ \omega =\dfrac{2\pi }{T};\omega =2\pi f $
Câu 20: Khi một vật chuyển động tròn đều, phát biểu nào sau đây là sai?
- A
- B
- C
- D
Góc quay được trong một đơn vị thời gian càng lớn thì tốc độ góc càng lớn.
Câu 21: Chọn câu đúng.
- A
- B
- C
- D
Công thức tốc độ góc. $ \omega =\dfrac{\Delta \alpha }{\Delta t} $
Câu 22: Chọn phương án sai trong các câu sau. Trong chuyển động tròn đều,
- A
- B
- C
- D
Chuyển động tròn đều có vectơ vận tốc thay đổi liên tục.
Câu 23: Chuyển động tròn đều không có đặc điểm nào sau đây?
- A
- B
- C
- D
Trong chuyển động tròn đều, vecto gia tốc luôn hướng vào tâm quỹ đạo.
Câu 24: Trong chuyển động tròn đều, gia tốc hướng tâm đặc trưng cho
- A
- B
- C
- D
Trong chuyển động tròn đều, gia tốc hướng tâm đặc trưng cho sự biến thiên về hướng của vectơ vận tốc
Câu 25: Điều nào sau đây là đúng khi nói về chu kì và tần số của vật chuyển động tròn đều?
- A
- B
- C
- D
Mối liên hệ giữa tần số và chu kỳ là $ f=\dfrac{1}{T} $
Câu 26: Các công thức liên hệ giữa vận tốc dài với vận tốc góc, và gia tốc hướng tâm với tốc độ dài của chất điểm chuyển động tròn đều là
- A
- B
- C
- D
Trong chuyển động tròn đều \[ v=\omega r;{{a}_{ht}}=\dfrac{{{v}^{2}}}{r} \].
Xem thêm các bài tiếp theo bên dưới