Thể tích vật thể tròn xoay quanh Oy
Lý thuyết về Thể tích vật thể tròn xoay quanh Oy
Hình phẳng tạo bởi : đường $x=f\left( y \right)\left( {{C}_{1}} \right)$, đường $x=g\left( y \right)\left( {{C}_{2}} \right)$, $y=c,y=d$. Khi đó thể tích của vật thể tròn xoay quay quanh trục $Oy$ là
$V=\pi \int_{c}^{d}{\left[ {{f}^{2}}\left( y \right)-{{g}^{2}}\left( y \right) \right]dy}$ $(g\left( y \right)\le f\left( y \right)$ với $\forall y\in \left[ c;d \right])$.
Ví dụ: Cho hình phẳng $\left( H \right)$ giới hạn bởi đường cong $x=\sqrt{y}$, trục tung và hai đường thẳng $y=1,y=4$. Tính thể tích khối tròn xoay tạo thành khi quay $\left( H \right)$ quanh trục $Oy$.
Lời giải
Thể tích khối tròn xoay quay quanh trục $Oy$ là
$V=\pi \int_{1}^{4}{\left[ {{\left( \sqrt{y} \right)}^{2}} \right]}dy=\pi \int_{1}^{4}{y}dy=\frac{15\pi }{2}$ (đvtt).
Bài tập tự luyện có đáp án
Câu 1: Trên mặt phẳng Oxy, cho hình phẳng (H) giới hạn bởi các đường $ y=3x-{{x}^{2}} $ và trục hoành. Thể tích khối tròn xoay khi quay (H) quanh tục Ox bằng:
- A
- B
- C
- D
Xét phương trình: $ 3x-{{x}^{2}}=0\Leftrightarrow \left[ \begin{matrix} x=0 \\ x=3 \\ \end{matrix}\Rightarrow V=\pi \int\limits_{0}^{3}{{{\left( 3x-{{x}^{2}} \right)}^{2}}dx}=\dfrac{81\pi }{10} \right. $
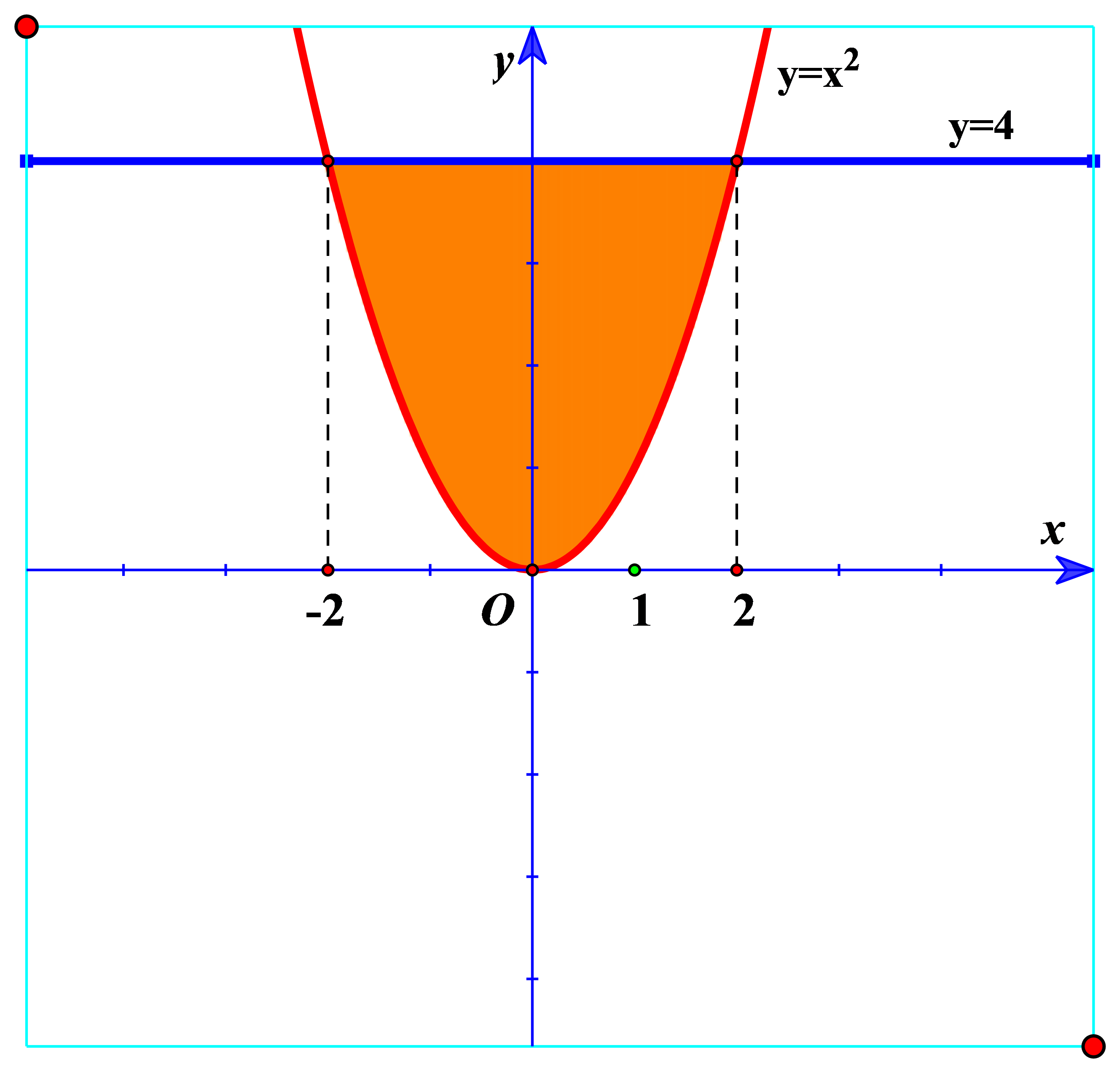
Câu 2: Hình phẳng giới hạn bởi đường cong $ y={{x}^{2}} $ và đường thẳng $ y=4 $ quay một vòng quanh trục Ox. Thể tích khối tròn xoay được sinh ra bằng:
- A
- B
- C
- D
Phương trình hoành độ giao điểm: $ {{x}^{2}}=4\Leftrightarrow x=\pm 2 $

Suy ra:
$ V=\pi \int\limits_{-2}^{2}{\left[ {{4}^{2}}-{{\left( {{x}^{2}} \right)}^{2}} \right]\mathrm{d}x}=\pi \int\limits_{-2}^{2}{\left( 16-{{x}^{4}} \right)\mathrm{d}x}=\left. \pi \left( 16x-\dfrac{{{x}^{5}}}{5} \right) \right|_{-2}^{2} $ $ =\dfrac{256}{5}\pi $
Câu 3: Thể tích của khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường $ y=\sqrt{x},y=x $ quanh trục Ox bằng:
- A
- B
- C
- D
Xét phương trình $ \sqrt{x}-x\Leftrightarrow \left\{ \begin{matrix} x\ge 0 \\ x-{{x}^{2}} \\ \end{matrix}\Rightarrow x=0;x=1 \right. $
Và $ \sqrt{x}\ge x\,\forall x\in \left[ 0;1 \right]\Rightarrow V=\pi \int\limits_{0}^{1}{\left( {{(\sqrt{x})}^{2}}-{{x}^{2}} \right)dx=\pi \int\limits_{0}^{1}{\left( x-{{x}^{2}} \right)dx}} $
Câu 4: Cho hình phẳng giới hạn (H) như hình vẽ bên. Thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) qaunh trục Oy là:


- A
- B
- C
- D
Ta có: $ g\left( y \right)\ge f\left( y \right) > 0;\,\,\forall y\in \left[ a;b \right]\,\,\Rightarrow $ $ V=\pi \int\limits_{b}^{a}{\left[ {{g}^{2}}\left( x \right)-{{f}^{2}}\left( x \right) \right]dy} $
Câu 5: Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường $ y=\dfrac{4}{x},y=0,x=1,x=4 $ quay quanh Ox là:
- A
- B
- C
- D
$ V=\pi \int\limits_{1}^{4}{\dfrac{16}{{{x}^{2}}}dx}=12\pi $
Câu 6: Cho hình phẳng trong hình (phần tô đậm) quay quah trục hoành. Thể tích khối tròn xoay tạo thành được tính theo công thức nào ?


- A
- B
- C
- D
Dựa vào hình vẽ ta được: $ V=\pi \int\limits_{a}^{b}{\left[ {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right]\text{d}x} $
Câu 7: Cho hình phẳng (D) được giới hạn bởi các đường $ x=0,x=1,y=0 $ và $ y=\sqrt{2x+1} $ . Thể tích V của khối tròn xoay tạo thành khi quay (D) xung quanh trục OX được tính theo công thức
- A
- B
- C
- D
Phương pháp: Quay hình phẳng được giới hạn bởi các đồ thị hàm số $ y=f\left( x \right);y=g\left( x \right) $ và các đườn thẳng $ x=a;x=b\left( a < b \right) $ quanh trục Ox ta được khối tròn xoay có thể tích được tính theo công thức: $ V=\pi \int\limits_{a}^{b}{\left| {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right|dx} $
Cách giải: Ta có $ V=\pi \int\limits_{0}^{1}{{{\left( \sqrt{2x+1} \right)}^{2}}dx=}\pi \int\limits_{0}^{1}{\left( 2x+1 \right)dx} $
Câu 8: Hình $ \left( H \right) $ giới hạn bởi các đường $ y=f\left( x \right) $ , $ x=a $ , $ x=b $ , $ \left( a < b \right) $ và trục $ Ox $ . Khi quay $ \left( H \right) $ quanh trục $ Ox $ ta được một khối tròn xoay có thể tích tính bằng công thức
- A
- B
- C
- D
Câu 9: Thể tích khối tròn xoay do phần hình phẳng S trong hình vẽ dưới quanh trục Ox được tính bằng công thức:


- A
- B
- C
- D
Ta có: $ {{f}_{1}}\left( x \right)\ge {{f}_{2}}\left( x \right) > 0;\,\forall x\in \left[ a;b \right]\,\,\Rightarrow V=\pi \int\limits_{a}^{b}{\left[ f_{1}^{2}\left( x \right)-f_{2}^{2}\left( x \right) \right]dx} $
Câu 10: Cho hình phẳng giới hạn (H) như hình vẽ bên. Thể tích khối tròn xoay sinh ra khi quay hình phẳng (H) quanh trục Ox là:


- A
- B
- C
- D
Ta có: $ f\left( x \right)\ge g\left( x \right) > 0;\,\forall x\in \left[ a;c \right];\,g\left( x \right)\ge f\left( x \right) > 0;\,\forall x\in \left[ c;b \right] $
$ V=\pi \int\limits_{a}^{c}{\left[ {{f}^{2}}\left( x \right)-{{g}^{2}}\left( x \right) \right]dx}+\pi \int\limits_{c}^{b}{\left[ {{g}^{2}}\left( x \right)-{{f}^{2}}\left( x \right) \right]dx} $
Câu 11: Thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường $ y=x{{e}^{x}}, $ $ y=0, $ $ x=0, $ $ x=1 $ xung quanh trục $ Ox $ là
- A
- B
- C
- D
$ V=\pi \int\limits_{0}^{1}{{{x}^{2}}{{e}^{2x}}\text{d}x}. $
Câu 12: Cho hình phẳng (H) giới hạn bởi đồ thị hàm số $ y={{x}^{2}}-2x+1,y=0,x=0,x=2 $ . Khối tròn xoay tạo thành khi quay hình phẳng (H) quanh trục Ox có thể tích là:
- A
- B
- C
- D
$ V=\pi \int\limits_{0}^{2}{{{\left( {{x}^{2}}-2x+1 \right)}^{2}}dx}=\dfrac{2}{5}\pi $
Câu 13: Cho hàm số $ y=f(x) $ xác định và liên tục trên $ \left[ a;b \right] $ . Gọi $ (D) $ là hình phẳng giới hạn bởi đồ thị hàm số $ y=f(x) $ trục hoành và hai đường thẳng $ x=a,\,x=b\,(a < b) $ . Thể tích khối tròn xoay được tạo thành khi quay $ (D) $ quanh trục $ Ox $ được tính theo công thức nào sau đây
- A
- B
- C
- D
Áp dụng công thức tính thể tích vật thể tròn xoay quay quanh trục $ Ox $ ta có $ V=\pi \int\limits_{a}^{b}{{{f}^{2}}(x)\text{d}x} $ .
Câu 14: Cho hình phẳng (H) giới hạn bởi đồ thị hàm số $ y=\dfrac{1}{x} $ , trục Ox và hai đường thẳng x = 1, x = 2. Khối tròn xoay tạo thành khi hình phẳng (H) quay quanh trục Ox có thể tích là:
- A
- B
- C
- D
Thể tích khối tròn xoay: $ V=\pi \int\limits_{1}^{2}{\dfrac{1}{{{x}^{2}}}dx}=-\dfrac{\pi }{x}\left| \begin{matrix} 2 \\ 1 \\ \end{matrix}=-\dfrac{\pi }{2}+\pi =\dfrac{\pi }{2} \right. $
Câu 15: Thể tích của khối tròn xoay khi quay hình phẳng D giới hạn bởi các đường $ y=\sqrt{x-2} $ , trục hoành, x = 3, x = 6 quanh trục Ox bằng:
- A
- B
- C
- D
$ V=\pi \int\limits_{3}^{6}{\left( x-2 \right)dx} $
Câu 16: Thể tích khối tròn xoay được giới hạn bởi các đường $ y=1-{{x}^{2}},y=0,x=0,x=2 $ khi quay quanh trục Ox bằng:
- A
- B
- C
- D
$ V=\pi \int\limits_{0}^{2}{{{\left( 1-{{x}^{2}} \right)}^{2}}dx}\to CASIO\to \dfrac{46\pi }{15} $
Xem thêm các bài tiếp theo bên dưới