Qui tắc tìm min-max trên 1 khoảng
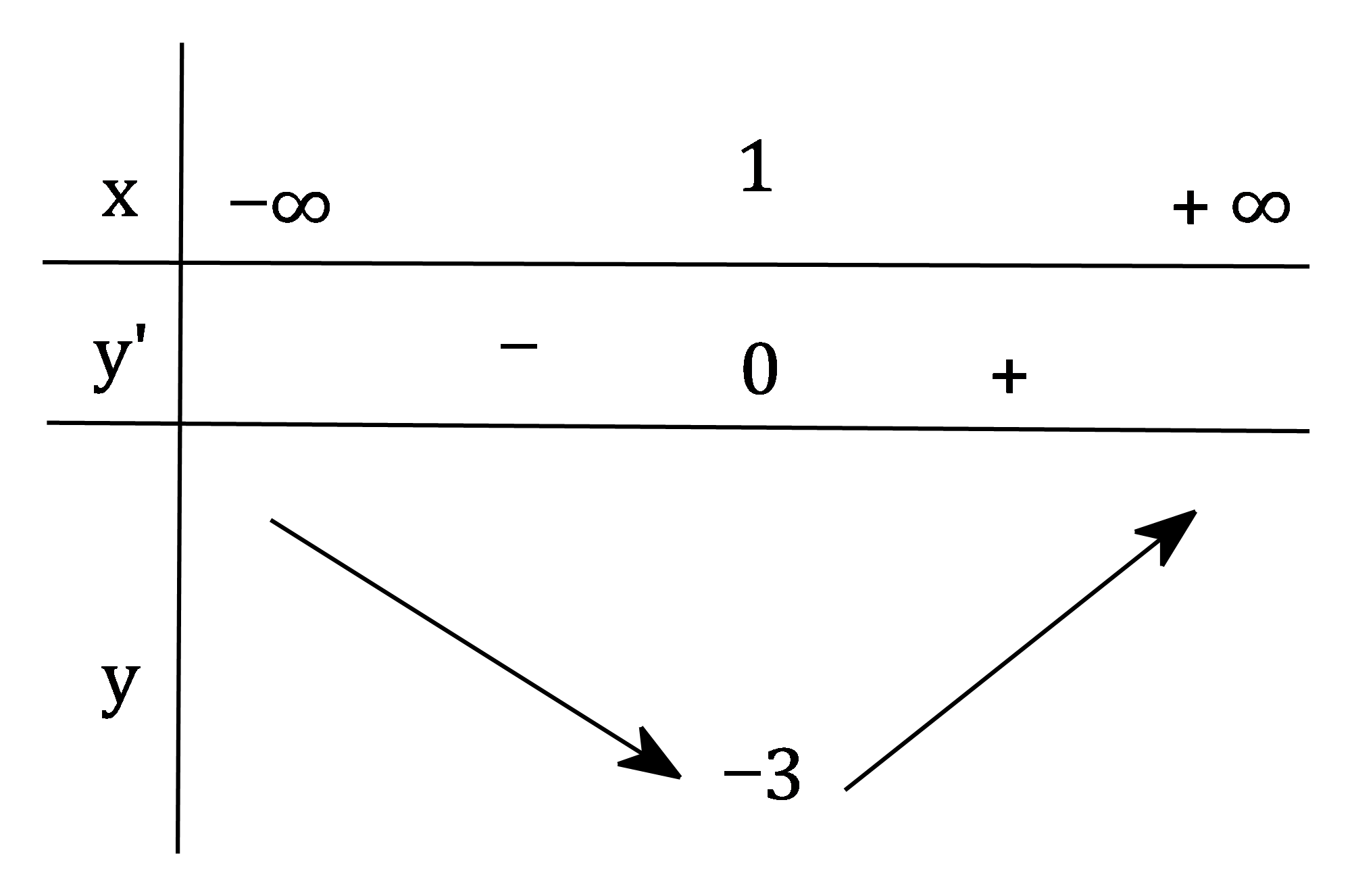
Lý thuyết về Qui tắc tìm min-max trên 1 khoảng
Qui tắc tìm min-max trên khoảng
B1. Tìm TXĐ
B2. Tính đạo hàm, xét dấu của đạo hàm
B3. Lập bảng biến thiên trên khoảng đang xét
B4. Kết luận min-max
Ví dụ. Tìm giá trị nhỏ nhất và giá trị lớn nhất của hàm số
$y=x-5+\dfrac{1}{x}$ trên khoảng $\left( 0;+\infty \right)$
Giải. Trên khoảng $\left( 0;+\infty \right)$ ta có $y'=1-\dfrac{1}{{{x}^{2}}}=\dfrac{{{x}^{2}}-1}{{{x}^{2}}}$
$y'=0\Leftrightarrow {{x}^{2}}-1=0\Leftrightarrow x=1$
Bảng biến thiên
Từ bảng biến thiên ta thấy trên khoảng $\left( 0;+\infty \right)$ hàm số có giá trị cực tiểu duy nhất, đó cũng là giá trị nhỏ nhất của hàm số
Vậy $\min\limits_{\left( 0;+\infty \right)}f\left( x \right)=-3$ (tại $x=1$). Không tồn tại giá trị lớn nhất của $f\left( x \right)$ trên khoảng $\left( 0;+\infty \right)$
Chú ý: Hàm số liên tục trên một khoảng có thể không có giá trị lớn nhất và giá trị nhỏ nhất trên khoảng đó. Chẳng hạn, hàm số $f\left( x \right)=\dfrac{1}{x}$ không có giá trị lớn nhất, giá trị nhỏ nhất trên khoảng $\left( 0;1 \right)$.
Bài tập tự luyện có đáp án
Câu 1: Cho $y=f\left( x \right)$ là hàm số nghịch biến trên khoảng $\left( a;b \right)$ và xác định trên đoạn $\left[ a;b \right]$ khi đó hàm số đạt giá trị lớn nhất trong đoạn $\left[ a;b \right]$ tại
- A
- B
- C
- D
Vì $y=f\left( x \right)$ là hàm số nghịch biến trên khoảng$\left( a;b \right)$ và xác định trên đoạn $\left[ a;b \right]$ nên \(f\left( x \right)\le f\left( a \right)\forall x\in \left[ a;b \right]\Rightarrow \underset{\left[ a;b \right]}{\mathop{\max f\left( x \right)}}\,=f\left( a \right)\)
Câu 2: Cho hàm số $y=f\left( x \right)$ luôn đồng biến trên $\left[ a;b \right]$. Giá trị lớn nhất của hàm số trên $\left[ a;b \right]$ là
- A
- B
- C
- D
Vì hàm số $y=f\left( x \right)$ luôn đồng biến trên $\left[ a;b \right]$ nên $f\left( a \right)\le f\left( x \right)\le f\left( b \right)$