Định nghĩa tích của một vectơ với một số
Lý thuyết về Định nghĩa tích của một vectơ với một số
Tích của vectơ →a→a với số thực k là một vectơ, kí hiệu là →ka−→ka được xác định như sau
1) Nếu k⩾0 thì vectơ →ka−→ka cùng hướng với vectơ→a→a
Nếu k<0 thì vectơ →ka−→ka ngược hướng với vectơ →a→a
2) Độ dài của vectơ →ka−→ka bằng |k|.∣→a→a∣
Phép lấy tích của vectơ với một số gọi là phép nhân vectơ với số (hoặc phép nhân số với vectơ)
Nhận xét: Từ định nghĩa ta thấy ngay 1→a→a=→a→a,(-1)→a→alà vectơ đối của →a→a, tức là (−1)→a→a=−→a→a
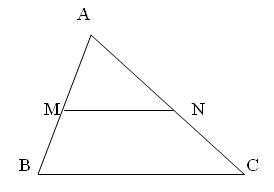
Vi dụ: Ta có tam giác ABC với M và N lần lượt là trung điểm hai cạnh AB và AC. Khi đó ta có:
a) →BC=2→MN;→MN=12→BC−−→BC=2−−−→MN;−−−→MN=12−−→BC
b) →BC=(−2)→NM;→MN=(−12)→CB−−→BC=(−2)−−−→NM;−−−→MN=(−12)−−→CB
c) →AB=2→MB;→AN=(−12)→CA−−→AB=2−−→MB;−−→AN=(−12)−−→CA
Bài tập tự luyện có đáp án
Câu 1: Cho tứ giác ABCDABCD . Gọi GG là trọng tâm của tam giác ABDABD , II là điểm trên GCGC sao cho IC=3IGIC=3IG . Với mọi điểm MM ta luôn có →MA+→MB+→MC+→MD−−→MA+−−→MB+−−→MC+−−→MD bằng:
- A
- B
- C
- D

Ta có: 3→IG=−→IC3−→IG=−−→IC .
Do GG là trọng tâm của tam giác ABDABD nên
→IA+→IB+→ID=3→IG⇔→IA+→IB+→ID=−→IC⇔→IA+→IB+→IC+→ID=→0
Khi đó: →MA+→MB+→MC+→MD
=→MI+→IA+→MI+→IB+→MI+→IC+→MI+→ID=4→MI+(→IA+→IB+→IC+→ID)=4→MI+→0=4→MI
Câu 2: Cho ngũ giác ABCDE . Gọi M,N,P,Q lần lượt là trung điểm các cạnh AB,BC,CD,DE . Gọi I và J lần lượt là trung điểm các đoạn MP và NQ . Khẳng định nào sau đây đúng ?
- A
- B
- C
- D

Ta có: 2→IJ=→IQ+→IN=→IM+→MQ+→IP+→PN=→MQ+→PN
{→MQ=→MA+→AE+→EQ→MQ=→MB+→BD+→DQ⇒2→MQ=→AE+→BD⇔→MQ=12(→AE+→BD) , →PN=−12→BD
Suy ra: 2→IJ=12(→AE+→BD)−12→BD=12→AE⇒→IJ=14→AE
Câu 3: Cho tam giác ABC và I thỏa mãn →IA=3→IB . Mệnh đề nào sau đây đúng?
- A
- B
- C
- D
Ta có
→IA=3→IB⇔→CA−→CI=3(→CB−→CI)
⇔2→CI=3→CB−→CA⇔→CI=12(3→CB−→CA).
Xem thêm các bài tiếp theo bên dưới