Tứ giác nội tiếp đường tròn
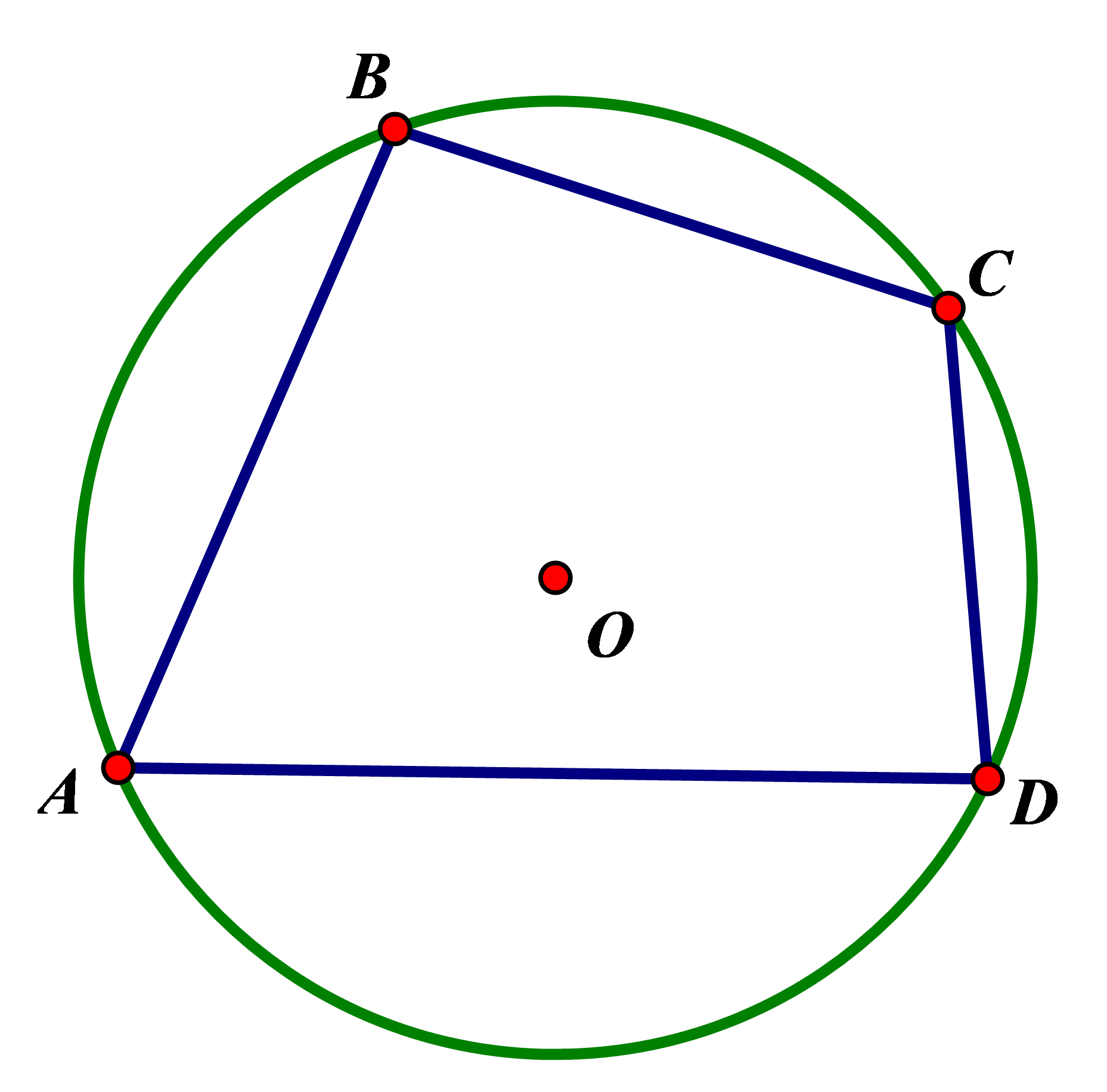
Lý thuyết về Tứ giác nội tiếp đường tròn
1. Định nghĩa tứ giác nội tiếp
Một tứ giác có bốn đỉnh nằm trên một đường tròn gọi là tứ giác nội tiếp đường tròn (gọi tắt là nội tiếp đường tròn).
2. Định lí
Trong một tứ giác nôị tiếp, tổng số đo hai góc đối diện bằng $180^0$
$ABCD$ nội tiếp đường tròn $(O)$
\[\left\{ {\begin{array}{*{20}{l}}
{\widehat A + \widehat C = {{180}^0}} \\
{\widehat B + \widehat D = {{180}^0}}
\end{array}} \right.\]
3. Định lí đảo
Nếu tứ giác có tổng số đo hai góc đối diện bằng $180^0$ thì tứ giác đó nội tiếp được đường tròn.
Bài tập tự luyện có đáp án
Câu 1: Tứ giác nào luôn nội tiếp đường tròn là
- A
- B
- C
- D
Hình chữ nhật luôn là tứ giác nội tiếp vì nó có $ 4 $ góc vuông nên tổng số đo hai góc đối luôn bằng $ {{180}^{0}} $ .
Các hình còn lại chưa đủ điều kiện để luôn là một tứ giác nội tiếp.
Câu 2: Cho nửa đường tròn $ (O;R) $ đường kính $ BC $ . Lấy điểm $ A $ trên tia đối của tia $ BC $ . Kẻ tiếp tuyến $ AF,Bx $ của nửa đường tròn $ (O) $ (với $ F $ là tiếp điểm). Tia $ AF $ cắt tia $ Bx $ của nửa đường tròn tại $ D $ . Khi đó tứ giác $ OBDF $ là
- A
- B
- C
- D
Ta có $ \widehat{DBO}={{90}^{0}} $ và $ \widehat{DFO}={{90}^{0}} $ ( tính chất tiếp tuyến).
Tứ giác $ OBDF $ có $ \widehat{DBO}+\widehat{DFO}={{90}^{0}}+{{90}^{0}}={{180}^{0}} $ nên nội tiếp trong một đường tròn.
Câu 3: Cho các hình vẽ dưới đây, tứ giác nào là tứ giác nội tiếp?


- A
- B
- C
- D
Hình 1 có tổng hai góc đối là: $ {{115}^{0}}+{{75}^{0}}={{190}^{0}}\ne {{180}^{0}} $ nên không là tứ giác nội tiếp.
Hình 2 có tổng hai góc đối là: $ {{92}^{0}}+{{85}^{0}}={{177}^{0}}\ne {{180}^{0}} $ nên không là tứ giác nội tiếp.
Hình 3 có tổng hai góc đối là: $ {{50}^{0}}+{{50}^{0}}={{100}^{0}}\ne {{180}^{0}} $ nên không là tứ giác nội tiếp.
Hình 4 có tổng hai góc đối là: $ {{90}^{o}}+{{90}^{o}}={{180}^{o}} $ nên là tứ giác nội tiếp.
Câu 4: Cho tứ giác $ ABCD $ nội tiếp. Chọn câu sai.
- A
- B
- C
- D
+) $ \widehat{ABD}=\widehat{ACD} $ (hai góc nội tiếp cùng chắn cung AD)
+) $ \hat{A}+\hat{B}+\hat{C}+\hat{D}={{360}^{0}} $ (tổng 4 góc trong tứ giác).
Câu 5: Cho tứ giác \[ ABCD \] nội tiếp đường tròn \[ (O) \] (hình \[ 1 \] ). Chọn khẳng định sai.


- A
- B
- C
- D
Vì tứ giác $ ABCD $ là tứ giác nội tiếp nên
$ \widehat{BDC}=\widehat{BAC} $ (hai góc nội tiếp cùng chắn cung $ BC $ )
$ \widehat{ABC}+\widehat{ADC}={{180}^{\circ }} $ (tổng hai góc đối bằng $ {{180}^{\circ }} $ )
$ \widehat{DCB}=\widehat{BAx} $ (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó).
Câu 6: Cho tứ giác ABCD nội tiếp đường tròn. Cho biết $ \widehat{A}={{115}^{0}}\,;\,\,\widehat{B}={{75}^{0}} $ , khi đó:
- A
- B
- C
- D
Tứ giác ABCD là tứ giác nội tiếp nên ta có:
$ +)\ \ \widehat{A}+\widehat{C}={{180}^{0}}\Rightarrow \widehat{C}={{180}^{0}}-\widehat{A}={{65}^{0}}. $
$ +)\ \ \ \widehat{B}+\widehat{D}={{180}^{0}}\Rightarrow \widehat{D}={{180}^{0}}-\widehat{B}={{105}^{0}} $ .
Câu 7: Tứ giác ở hình nào dưới đây là tứ giác nội tiếp ?

- A
- B
- C
- D
Hình 2 sai vì $ \hat{A}+\hat{C}={{115}^{0}}+{{75}^{0}}={{190}^{0}}\ne {{180}^{0}} $
Hình 3 sai vì $ \hat{C}+\hat{B}={{92}^{0}}+{{85}^{0}}={{177}^{0}}\ne {{180}^{0}} $ .
Hình 5 sai vì $ \hat{D}+\hat{B}={{50}^{0}}+{{50}^{0}}={{100}^{0}}\ne {{180}^{0}} $ .
Hình 4 đúng vì tứ giác này có $ 4 $ đỉnh cùng thuộc một đường tròn.
Câu 8: Một tứ giác nội tiếp đường tròn nếu có:
- A
- B
- C
- D
Một tứ giác nội tiếp đường tròn nếu tứ giác đó có tổng hai góc đối bằng $ {{180}^{0}} $ hay nó có hai góc đối bù nhau.
Câu 9: Cho tứ giác $ ABCD $ nội tiếp đường tròn $ \left( O \right) $ . Chọn khẳng định sai?


- A
- B
- C
- D
Vì tứ giác $ ABCD $ là tứ giác nội tiếp nên
$ \widehat{BDC}=\widehat{BAC} $ (hai góc nội tiếp cùng chắn cung $ BC $ ).
$ \widehat{ABC}+\widehat{ADC}=180{}^\circ $ (tổng hai góc đối bằng $ 180{}^\circ $ ).
$ \widehat{DCB}=\widehat{BAx} $ (góc ngoài tại một đỉnh bằng góc trong tại đỉnh đối với đỉnh đó).
Do đó $ \widehat{BCA}=\widehat{BAx} $ là khẳng định sai.
Xem thêm các bài tiếp theo bên dưới