Hợp lực do nhiều điện tích tác dụng lên một điện tích

Bài sau

4.4/5

Tác giả: Thầy Tùng

Đăng ngày: 11 Aug 2022

Lưu về Facebook:

Hình minh họa Hợp lực do nhiều điện tích tác dụng lên một điện tích

MỤC LỤC

Lý thuyết

Bài tập

Lý thuyết về Hợp lực do nhiều điện tích tác dụng lên một điện tích

Điện tích chịu tác dụng của 2 hay nhiều điện tích:

$\overrightarrow{F}=\overrightarrow{{{F}_{1}}}+\overrightarrow{{{F}_{2}}}+..\overrightarrow{{{F}_{n}}}$

Các bước tìm hợp lực ${{\vec{F}}_{o}}$ do các điện tích ${{q}_{1}};{{q}_{2}};...$ tác dụng lên điện tích ${{q}_{o}}$ :

Bước 1: Xác định vị trí điểm đặt các điện tích (vẽ hình).

Bước 2: Tính độ lớn các lực ${{F}_{10}};{{F}_{20}}...$ , Fno lần lượt do q1 và q2 tác dụng lên qo.

Bước 3: Vẽ hình các vectơ lực ${{\vec{F}}_{10}};{{\vec{F}}_{20}}....$

Bước 4: Từ hình vẽ xác định phương, chiều, độ lớn của hợp lực ${{\vec{F}}_{o}}$ .

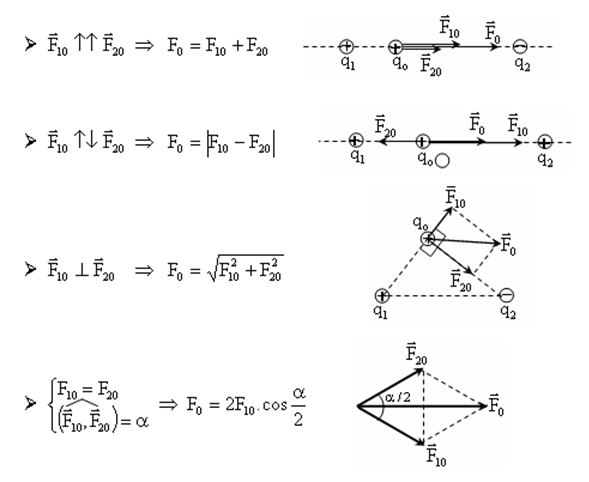
Các trường hợp đặc biệt:

Góc $\alpha$ bất kì: $\alpha$ là góc hợp bởi hai vectơ lực.

$F_{0}^{2}=F_{10}^{2}+F_{20}^{2}+2F_{10}^{{}}F_{20}^{{}}.\cos \alpha$ $\Rightarrow \left| {{F}_{1}}-{{F}_{2}} \right|\le F\le {{F}_{1}}+{{F}_{2}}$

Bài sau

Bài tập tự luyện có đáp án

Câu 1: Điện tích q chịu tác dụng của 2 lực điện có độ lớn 5N và 10N. Lực điện tổng hợp tác dụng lên điện tích q không thể nhận giá trị nào sau đây ?

A
8N
B
4N
C
14N
D
12N

Bấm vào đây để xem đáp án chi tiết

Lực điện tổng hợp tác dụng lên điện tích q thỏa mãn:

$\left| 10-5 \right|\le F\le 10+5 \Leftrightarrow 5\le F\le 15$

Vậy lực điện tổng hợp tác dụng lên điện tích q không thể là 4N.

Câu 2: Cho hai điện tích điểm ${ q _ 1 },{ q _ 2 }$ có độ lớn bằng nhau và cùng dấu, đặt trong không khí và cách nhau một khoảng r. Đặt điện tích điểm ${ q _ 3 }$ tại trung điểm đoạn thẳng nối hai điện tích ${ q _ 1 },{ q _ 2 }$ . Lực tác dụng lên điện tích ${ q _ 3 }$ là:

A
$F=0$
B
$F=k\dfrac{\left| { q _ 1 }{ q _ 2 } \right|}{{ r ^ 2 }}$
C
$F=k\dfrac{\left| { q _ 1 }{ q _ 3 } \right|}{{ r ^ 2 }}$
D
$F=4k\dfrac{\left| { q _ 1 }{ q _ 2 } \right|}{{ r ^ 2 }}$

Bấm vào đây để xem đáp án chi tiết

+ Ta có: ${ F _{13}}={ F _{23}}$

+ $\overrightarrow{{ F _{13}}}\uparrow \downarrow \overrightarrow{{ F _{23}}}\Rightarrow F={ F _{13}}-{ F _{23}}=0$

Câu 3: Điện tích q chịu tác dụng của 2 lực điện có độ lớn 8N và 2N. Lực điện tổng hợp tác dụng lên điện tích q không thể nhận giá trị nào sau đây ?

A
7N
B
12N
C
9N
D
8N

Bấm vào đây để xem đáp án chi tiết

Lực điện tổng hợp tác dụng lên điện tích q thỏa mãn:

$\left| 2-8 \right|\le F\le 8+2 \Leftrightarrow 6\le F\le 10$

Vậy lực điện tổng hợp tác dụng lên điện tích q không thể là 12N.

Câu 4: Tại hai điểm A và B có hai điện tích $q_A,q_B$ . Tại điểm M một êlectron được thả ra không có vận tốc ban đầu thì electron di chuyển theo hướng ra xa các điện tích. Tình huống nào sau đây không thể xảy ra?

A
$q_A<0,q_B>0$ .
B
$q_A>0,q_B<0$ .
C
$q_A >0,q_B>0$ .
D
$\left| {{q_A}} \right| = \left| {{q_B}} \right|.$

Bấm vào đây để xem đáp án chi tiết

Tình huống không thể xảy ra khi e bị hút về phía hai điện tích tức là hợp lực có hướng về hai điện tích A và B hay hai điện tích A và B là cùng dấu.

Câu 5: Có 3 điện tích điểm ${ q _ 1 },{ q _ 2 },{ q _ 3 }$ đặt trong không khí. ${ q _ 3 }$ chịu tác dụng của lực điện $\overrightarrow{{ F _{13}}};\overrightarrow{{ F _{23}}}$ lần lượt do ${ q _ 1 };{ q _ 2 }$ gây ra. Khi đó lực điện tổng hợp tác dụng lên điện tích ${ q _ 3 }$ được xác định bởi biểu thức nào sau đây?

A
$\overrightarrow{{ F _ 3 }}=\overrightarrow{{ F _{13}}}-\overrightarrow{{ F _{23}}}$
B
${ F _ 3 }={ F _{13}}-{ F _{23}}$
C
${ F _ 3 }={ F _{13}}+{ F _{23}}$
D
$\overrightarrow{{ F _ 3 }}=\overrightarrow{{ F _{13}}}+\overrightarrow{{ F _{23}}}$

Bấm vào đây để xem đáp án chi tiết

Lực điện tổng hợp tác dụng lên điện tích ${ q _ 3 }$ được xác định theo quy tác tổng hợp lực ( tổng hợp vec tơ lực)

$\overrightarrow{{ F _ 3 }}=\overrightarrow{{ F _{13}}}+\overrightarrow{{ F _{23}}}$

Xem thêm các bài tiếp theo bên dưới

Hợp lực do nhiều điện tích tác dụng lên một điện tích

Lý thuyết về Hợp lực do nhiều điện tích tác dụng lên một điện tích

Bài tập tự luyện có đáp án

Câu 1: Điện tích q chịu tác dụng của 2 lực điện có độ lớn 5N và 10N. Lực điện tổng hợp tác dụng lên điện tích q không thể nhận giá trị nào sau đây ?

Câu 3: Điện tích q chịu tác dụng của 2 lực điện có độ lớn 8N và 2N. Lực điện tổng hợp tác dụng lên điện tích q không thể nhận giá trị nào sau đây ?

Câu 4: Tại hai điểm A và B có hai điện tích qA,qBqA,qBq_A,q_B. Tại điểm M một êlectron được thả ra không có vận tốc ban đầu thì electron di chuyển theo hướng ra xa các điện tích. Tình huống nào sau đây không thể xảy ra?

Câu 4: Tại hai điểm A và B có hai điện tích $q_A,q_B$ . Tại điểm M một êlectron được thả ra không có vận tốc ban đầu thì electron di chuyển theo hướng ra xa các điện tích. Tình huống nào sau đây không thể xảy ra?