Định nghĩa số phức
Lý thuyết về Định nghĩa số phức
Mỗi biểu thức dạng $a+bi$, trong đó $a,b\in \mathbb{R}$, và số $i$ thỏa mãn $i^2 = -1$ được gọi là một số phức.
- $a$ là phần thực
- $b$ là phần ảo
Tập hợp các số phức kí hiệu $\mathbb{C}$
Ví dụ. Các số sau là những số phức: $2+5i;\,\,\,-\sqrt{2}+3i;\,\,\,1+\left( -3 \right)i;\,\,\,1+\sqrt{3}i;\,\,\,3i;\,\,\,-1$.
Chú ý.
- Số phức có phần ảo bằng $0$ ($z = a + 0i$) được coi là số thực
- Số phức có phần thực bằng $0$ ($z = 0 + bi$) được gọi là số ảo (hay số thuần ảo).
- Số $0$ vừa là số thực vừa là số ảo.
Hai số phức bằng nhau
Hai số phức được gọi là bằng nhau nếu phần thực và phần ảo của chúng tương ứng bằng nhau.
Cụ thể, nếu $ z = a + bi,(a, b \in \mathbb{R}) $ và $ z' = a' + b'i,(a', b' \in \mathbb{R})$ được gọi là bằng nhau khi và chỉ khi $$a = a', b = b'.$$Ví dụ. Tìm các số thực $x$ và $y$, biết: $$\left( 2x+1 \right)+\left( 3y-2 \right)i=\left( x+2 \right)+\left( y+4 \right)i. $$Giải. Từ định nghĩa của hai số phức bằng nhau ta có: $\left\{\begin{array}{l} 2x+1=x+2\\ 3y-2=y+4\end{array}\right. \Leftrightarrow \left\{\begin{array}{l} x = 1\\ y = 3\end{array}\right.$.
Điểm biểu diễn số phức
Trong hệ trục tọa độ $Oxy$
- Với mỗi $z = a + bi\,\,\, (a, b \in \mathbb{R})$ ta đặt tương ứng điểm $M(a;b)$
- Với mỗi $M(a;b)$ là điểm biểu diễn một số phức $z = a + bi$.
- $Ox$ được gọi là trục thực
- $Oy$ được gọi là trục ảo
Vectơ $\vec{u}$ có tọa độ $(a; b)$ biểu diễn $z = a + bi$.
$M$ biểu diễn số phức $z$ cũng có nghĩa là vectơ $\overrightarrow{OM}$ biểu diễn số phức đó.
Nếu $\overrightarrow{u}, \overrightarrow{u}'$ theo thứ tự biểu diễn các số phức $z, z'$ thì:
- $\overrightarrow{u} + \overrightarrow{u}'$ biểu diễn số phức $z + z'$.
- $\overrightarrow{u} - \overrightarrow{u}'$ biểu diễn số phức $z - z'$.
Số phức liên hợp
Cho số phức $z=a+bi (a,b \in \mathbb{R})$. Ta gọi số phức $a-bi$ là số phức liên hợp của z và kí hiệu là $\bar{z}$. $$z = a + bi \Rightarrow \bar{z} = a - bi.$$Ta có các tính chất sau của số phức liên hợp:$\overline{\bar{z}} = z$.$\overline{z \pm z'} = \overline{z} \pm \overline{z'}$.$\overline{z \cdot z'} = \overline{z} \cdot \overline{z'}$.$\overline{\left(\dfrac{z}{z'}\right)} = \dfrac{\overline{z}}{\overline{z'}} (z' \ne 0)$.
Mô đun số phức
Định nghĩa: Môđun của số phức $z = a + bi (a, b \in \mathbb{R})$, kí hiệu là $|z|$ hoặc $|a + bi|$, là một số thực không âm cho bởi công thức $\left| a+bi \right|=\sqrt[{}]{{{a}^{2}}+{{b}^{2}}}$.
Từ đó ta có thể suy ra $z \bar{z} = |z|^2$ và $|\bar{z}| = |z|$ với mọi số phức $z$.
Nếu $z \in \mathbb{R}$ ($z$ là số thực) thì môđun của $z$ chính là giá trị tuyệt đối của số thực đó và $|z| = 0 \Leftrightarrow z = 0$.
Ví dụ. $\left| 3-2i \right|=\sqrt[{}]{{{3}^{2}}+{{\left( -2 \right)}^{2}}}=\sqrt[{}]{13}$
Tính chất: Với hai số phức $z_1, z_2$ bất kỳ ta có:
$|z_1 + z_2| \le |z_1| + |z_2|$.
Đẳng thức xảy ra khi và chỉ khi có ít nhất một trong hai số bằng $0$ hoặc tồn tại số thực $k \ne 0$ sao cho $z_1 = k \cdot z_2$
$|z_1 - z_2| \ge \Big| |z_1| - |z_2| \Big|$.
Đẳng thức xảy ra khi và chỉ khi có ít nhất một trong hai số bằng $0$ hoặc tồn tại số thực $k \ne 0$ sao cho $z_1 = k \cdot z_2$
$| z_1 \cdot z_2| = |z_1| \cdot |z_2|$.$\left|\dfrac{z_1}{z_2}\right| = \dfrac{|z_1|}{|z_2|}$ (với $z_2 \ne 0$).
Bài tập tự luyện có đáp án
Câu 1: Cho số phức $ z=a+bi $ . Số phức $ {{z}^{2}} $ có phần thực là:
- A
- B
- C
- D
Câu 2: Khẳng định sai trong các khẳng định sau:
- A
- B
- C
- D
$\mathbb{N}$ là tập số tự nhiên, $\mathbb{Z}$ là tập số nguyên, $\mathbb{Q}$ là tập số hữu tỷ, $\mathbb{R}$ là tập số thực và $\mathbb{C}$ là tập số phức. Ta có mỗi liên hệ là: $\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}\subset \mathbb{C}$.
Vậy chọn đáp án $\mathbb{C}\subset \mathbb{Q}$
Câu 3: Cho số phức $z=1-3i$ . Khẳng định nào sau đây là sai?
- A
- B
- C
- D
Ta có $\left| z \right|=\sqrt{1+9}=\sqrt{10}$. Vậy khẳng định “$\left| z \right|=10$” sai
Câu 4: Số nào sau đây là số thuần ảo
- A
- B
- C
- D
Ta có $\left( 2-3i \right)+\left( 2{{i}^{2}}-3i \right)=-6i$ là số thuần ảo
Câu 5: Cho số phức \[z=a+bi\]. Số phức ${{z}^{2}}$ có phần thực là:
Cho số phức \[z=a+bi\]. Số phức ${{z}^{2}}$ có phần thực là:
- A
- B
- C
- D
\[{z^2} = {a^2} - {b^2} + 2abi\]
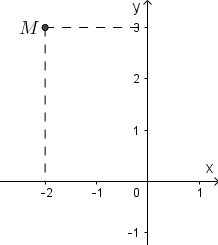
Câu 6: Điểm \[M\] trong hình vẽ bên là điểm biểu diễn của số phức \[z\] có môđun bằng


- A
- B
- C
- D
Điểm \[M\] trong hình vẽ biểu diễn cho số phức \[z=-2+3i\Rightarrow \left| z \right|=\sqrt{13}\].
Câu 7: Nghịch đảo của số phức $z=i$ là
- A
- B
- C
- D
Ta có $\dfrac{1}{z}=-i$
Câu 8: Cho $z=3-4i$, khẳng định nào sau đây là sai :
- A
- B
- C
- D
Ta có $zi=4+3i$ suy ra chọn đáp án $zi=4-3i$
Câu 9: Cho số phức $z=1-i+{{i}^{3}}$. Tìm phần thực $a$ và phần ảo $b$ của $z$.
Cho số phức $z=1-i+{{i}^{3}}$. Tìm phần thực $a$ và phần ảo $b$ của $z$.
- A
- B
- C
- D
Ta có $z=1-i+{{i}^{3}}=1-2i$ Vậy phần thực của z là 1 , phần ảo là -2
Câu 10: Môđun của số phức $z={{\left( 1+i \right)}^{3}}$ là
- A
- B
- C
- D
Dùng Casio tính được $\left| z \right|=\left| {{\left( 1+i \right)}^{3}} \right|=2\sqrt{2}$
Câu 11: Biết \(z={{\left( 1+2i \right)}^{2}}\), phần thực và ảo của số phức $\overline{\overline{z}}$ là:
- A
- B
- C
- D
Ta có \(\overline{\overline{z}}=z\)
\(z={{\left( 1+2i \right)}^{2}}=-3+4i\)
Vậy phần thực là $-3$ , phần ảo là 4
Câu 12: Số phức \(z={{\left( 2-\sqrt{3}i \right)}^{2}}\) thu gọn ta được:
- A
- B
- C
- D
Cách 1.\(z={{\left( 2-\sqrt{3}i \right)}^{2}}={{2}^{2}}-4\sqrt{3}i-3=1-4\sqrt{3}i\)
Cách 2. Dùng casio.
Câu 13: Điểm biểu diễn số phức liên hợp của số phức $ z=2-3i $ là
- A
- B
- C
- D
Số phức liên hợp của $ z=2-3i $ là $ \overline{z}=2+3i $ . Vậy điểm biểu diễn số phức $ \overline{z} $ là $ M\left( 2\,;\,3 \right) $ .
Câu 14: Cho hai số phức $z,z'$. Khẳng định sai là:
- A
- B
- C
- D
Ta giả sử $z=a+bi\left( a,b\in \mathbb{R} \right)$:
- Có $\overline{\overline{z}}=\overline{a-bi}=a+bi=z$.
- $|\overline{z}|=\sqrt{{{a}^{2}}+{{b}^{2}}}=|z|$.
- $\overline{z+z'}=a+a'-\left( b+b' \right)i=a-bi+a'-b'i=\overline{z}+\overline{z'}$.
- $z$ là số thuần ảo vậy $z$ có dạng $z=bi$ khi đó $\overline{z}=-bi \ne z$ khi $b \ne 0$.
Câu 15: Số phức liên hợp của số phức $ 3-4i $ là
- A
- B
- C
- D
$ z=3-4i\Rightarrow \overline{z}=3+4i $ .
Câu 16: Số phức nghịch đảo của số phức $z=-i$ là
- A
- B
- C
- D
Số phức nghịch đảo của số phức $z$ là $\dfrac{1}{z}=\dfrac{1}{-i}=i$
Câu 17: Môđun của số phức $ z=3-2i $ bằng
- A
- B
- C
- D
Ta có môdun của $ z=3-2i $ là $ |z|=\sqrt{3^2+2^2} =\sqrt{13}$.
Câu 18: Số phức \[z=\left( 2-i \right)+2\left( -1-i \right)\] là
- A
- B
- C
- D
Ta có $z=\left( 2-i \right)+2\left( -1-i \right)=-3i\Rightarrow z$ là số thuần ảo.
Câu 19: Cho số phức $z=2-3i$. Tìm phần thực a của z.
- A
- B
- C
- D
Có công thức z=a+bi nên a=2 và b=-3
Câu 20: Số phức nào dưới đây là số thuần ảo?
- A
- B
- C
- D
Số phức thuần ảo là số phức có phần thực bằng 0nên chọn $z=3i$
Câu 21: Trong các số phức sau, số phức nào có môđun nhỏ hơn \(3\) ?
- A
- B
- C
- D
Ta có $\left| 1+2i \right|=\sqrt{5}<3$
Câu 22: Chọn khẳng định sai trong các khẳng định sau?
- A
- B
- C
- D
Số 0 không có nghịch đảo nên khẳng định “Số phức nào cũng có số phức nghịch đảo” là sai.
Câu 23: Cho số phức $z=4-3i$. Tìm phần thực và phần ảo của số phức $\overline{z+1}$
- A
- B
- C
- D
$\overline{z+1}=5+3i$ nên số phức $\overline{z+1}$ có phần thực bằng $5$ phần ảo bằng 3.
Câu 24: Cho số phức z, khẳng định sai là:
- A
- B
- C
- D
Gọi $z=a+bi\left( a,b\in \mathbb{R} \right)$, ta có
\(\begin{array}{l} {z^2} = {\left( {a + bi} \right)^2} = {a^2} - {b^2} + 2{\rm{a}}bi\\ {\left| z \right|^2} = {a^2} + {b^2}\\ \Rightarrow {z^2} \ne {\left| z \right|^2} \end{array}\)