Khoảng cách giữa hai đường thẳng chéo nhau
Lý thuyết về Khoảng cách giữa hai đường thẳng chéo nhau
Phương pháp tính khoảng cách giữa hai đường thẳng chéo nhau dd và dd
Cách 1:
+ Xác định đường thẳng vuông góc chung của dd và dd
+ Tính độ dài đoạn vuông góc chung.
Cách 2:
+ Tìm (P)(P) chứa dd và song song với dd
+ Khi đó d(d,d′)=d(d,(P))=d(A,(P)) với A là một điểm bất kỳ thuộc d.
Chú ý: (P) có thể có sẵn hoặc chúng ta phải dựng (Cách dựng: qua một điểm B∈d′ dựng đường thẳng Δ song song vớid, lúc đó (P)≡(d,Δ)).
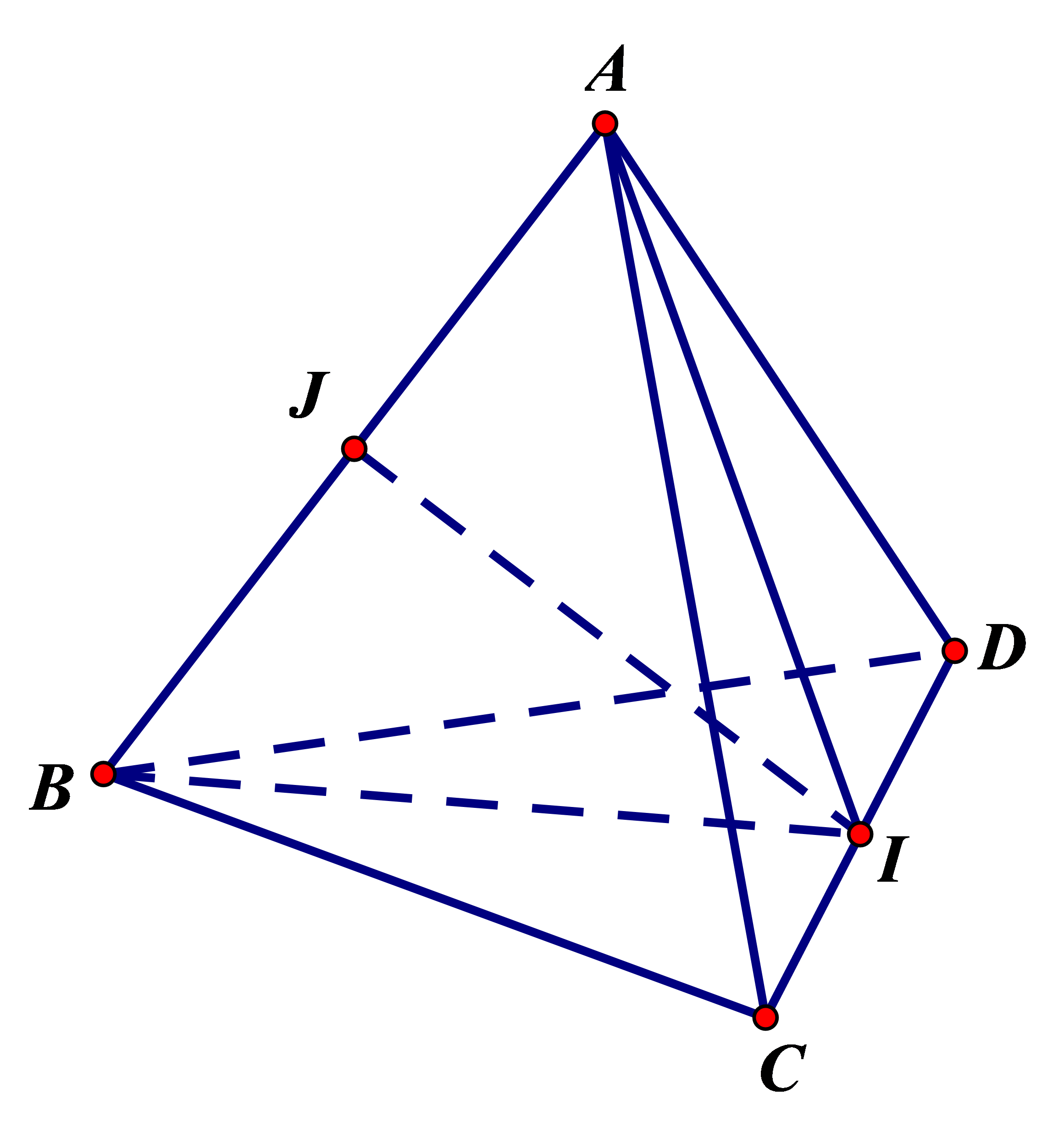
Ví dụ: Cho tứ diện ABCD có AB=a, tất cả các cạnh còn lại bằng 3a. Tính d(AB,CD)
Giải:
Gọi I,J lần lượt là trung điểm của CD và AB.
Vì ACD và ACD là các tam giác đều nên: CD⊥AI,CD⊥BI⇒CD⊥(AIB)⇒CD⊥IJ (1)
Mặt khác, ΔACD=ΔACD nên tam giác
AIB cân tại I. Do đó, IJ⊥AB (2)
+ Từ (1),(2) suy ra: IJ là đường vuông góc chung của AB và CD.
+ Ta có: IJ=√AI2−AJ2=√(3a√32)2−(a2)2=a√262.
Vậy d(AB,CD)=a√262
Bài tập tự luyện có đáp án
Câu 1: Khoảng cách giữa hai đường thẳng chéo nhau a và b bằng:
- A
- B
- C
- D
Khoảng cách giữa một trong hai đường thẳng đó đến mặt phẳng song song với nó và chứa đường thẳng còn lại.
Câu 2: Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng 1 (đvd). Khoảng cách giữaAA′ và BD′ bằng:
- A
- B
- C
- D

Ta có : AA′//BB′⇒AA′//(DBB′D′)
⇒d(AA ′,BD' )=d(A,(DBB′D′))=AO=√22.
Câu 3: Cho hình chóp S.ABCD có ABCD là hình vuông cạnh a,SA⊥(ABCD) và SA=a. Độ dài đoạn vuông góc chung của SB và CD bằng:
- A
- B
- C
- D
Độ dài đoạn vuông góc chung bằng khoảng cách hai đường thẳng SB,CD bằngBC=a
Câu 4: Trong các mệnh đề sau đây, mệnh đề nào là sai?
- A
- B
- C
- D
Câu 5: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O cạnh bằng a,SA vuông góc với đáy(ABCD), SA=a. khoảng cách giữa hai đường thẳng SC và BD bằng bao nhiêu?
- A
- B
- C
- D

Dựng OK⊥SC ,d(BD,SC)=OK=SA.OCSC=a.√22aa√3=a√6.
Câu 6: Trong các mệnh đề sau, mệnh đề nào đúng?
- A
- B
- C
- D
Câu 7: Cho hình chóp S.ABCD có đáy ABCD là hình vuông tâm O, SA vuông góc với đáyo (ABCD). Gọi K,H,M theo thứ tự là hình chiếu vuông góc của B,O,D lên SC. Đoạn vuông góc chung của hai đường thẳng SC và BD là đoạn thẳng nào dưới đây?
- A
- B
- C
- D
Chứng minh được OH⊥BD,OH⊥SC
Câu 8: Cho hình lập phương ABCD.A′B′C′D′ có cạnh bằng a. Tính khoảng cách h giữa hai đường thẳng BB′ và AC.
- A
- B
- C
- D

GọiOlà tâm của mặt đáyABCD. Khi đó ta cóOBchính là đường vuông góc chung củaBB1vàAC. Khi đó ta có :h=OA=a√2.
Câu 9: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy,SA=a. Khoảng cách giữa hai đường thẳngSBvàCDnhận giá trị nào trong các giá trị sau?
- A
- B
- C
- D

Ta có:d(CD,SB)=d(CD,(SAB))=AD=a.
Câu 10: Trong các mệnh đề sau, mệnh đề nào là đúng?
- A
- B
- C
- D
Câu 11: Cho tứ diện OABC, trong đó OA, OB, OC đôi một vuông góc với nhau và OA=OB=OC=a. Khoảng cách giữa OA và BC bằng bao nhiêu?
- A
- B
- C
- D
Gọi K là trung điểm BC,OK⊥BC,d(OA,BC)=OK=a√2.
Câu 12: Tìm mệnh đề sai trong các mệnh đề sau đây?
- A
- B
- C
- D
Câu 13: Cho hình chóp S.ABCD có đáy là hình vuông cạnh a. Đường thẳng SA vuông góc với mặt phẳng đáy,SA=a. Khoảng cách giữa hai đường thẳngSBvàCDnhận giá trị nào trong các giá trị sau?
- A
- B
- C
- D

Ta có:d(CD,SB)=d(CD,(SAB))=AD=a.
Câu 14: Cho hình chóp S.ABCDcó đáy ABCD là hình chữ nhật với AC=a√5, BC=a√2 . Đường thẳng SA vuông góc với mặt phẳng đáy. Tính khoảng cách giữa SD và BC.
- A
- B
- C
- D
Khoảng cách giữa SD và BC: d(BC,SD)=CD=a√3.
Câu 15: Trong các mệnh đề sau, mệnh đề nào đúng?
- A
- B
- C
- D
Đáp án (I): Đúng
Đáp án (II): Sai, do phát biểu này thiếu yếu tố cắt nhau.
Đáp án (III): Sai, vì mặt phẳng đó chưa chắc đã tồn tại.
Đáp án (IV): Sai, do phát biểu này thiếu yếu tố vuông góc.
Câu 16: Khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a là :
- A
- B
- C
- D

Gọi M là trung điểmDC , H là hình chiếu vuông góc của M lênd(A,(SCD))=AH;1AH2=16a2+13a2=12a2⇒AH=a√2 .
Ta có: {BM⊥CDAM⊥CD⇒CD⊥(ABM) {CD⊥MHAB⊥MH⇒MH=d(AB,CD) MH=2SABMAB=a√22
Câu 17: Cho hình hộp ABCD.A′B′C′D′có AB=AA=AD=a và A^′AB=^A′AD=^BAD=600. Khi đó khoảng cách giữa các đường thẳng chứa các cạnh đối của tứ diện A′.ABD bằng:
- A
- B
- C
- D
Câu 18: Cho khối lập phương ABCD.A′B′C′D′. Đoạn vuông góc chung của hai đường thẳng chéo nhau AD và A′C′ là :
- A
- B
- C
- D

{AA′⊥(A′B′C′D′)A′C′⊂(A′B′C′D′)→AA′⊥A′C′
{AA′⊥(ABCD)AD⊂(ABCD→AA′⊥AD
Câu 19: Trong các mệnh đề sau, mệnh đề nào đúng?
- A
- B
- C
- D
Câu 20: Khoảng cách giữa hai cạnh đối trong một tứ diện đều cạnh a bằng:
- A
- B
- C
- D

Gọi M,N lần lượt là trung điểm AB,CD.
d(AB,CD)=MN=√AN2−AM2=√AD2−CD24−AB24=√4a2−a2−a22=a√22.
Câu 21: Cho hình hộp chữ nhật ABCD.A′B′C′D′ có AB=a,BC=b,CC′=c. Khoảng cách giữa hai đường thẳngBB′vàAC′ là?
- A
- B
- C
- D

Dựng BH⊥AC. d(BB′,AC′)=BH=BA.BCAC=a.b√a2+b2.
Xem thêm các bài tiếp theo bên dưới