Dao động điện từ tự do
Lý thuyết về Dao động điện từ tự do
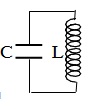
Một cuộn cảm có độ tự cảm L mắc với một tụ điện có điện dung C thành một mạch kín gọi là mạch dao động.
Nếu điện trở của mạch rất nhỏ, coi như bằng không, thì mạch là một mạch dao động lí tưởng.
Nghiên cứu về mặt lí thuyết sự biến thiên điện tích của một bản nhất định ( bản trên tụ điện trong hình vẽ dưới) của mạch dao động ta thu được kết quả sau:
Điện tích tức thời $q={{q}_{0}}cos(\omega t+\varphi )$
Hiệu điện thế (điện áp) tức thời $u=\dfrac{q}{C}=\dfrac{{{q}_{0}}}{C}c\text{os}(\omega t+\varphi )={{U}_{0}}c\text{os}(\omega t+\varphi )$
Dòng điện tức thời $i=q=-\omega {{q}_{0}}sin(\omega t+\varphi )={{I}_{0}}cos(\omega t+\varphi +\dfrac{\pi }{2})$
Điện tích q của một bản tụ điện và cường độ dòng điện I trong mạch dao động biến thiên điều hòa theo thời gian; i sớm pha hơn q một góc $\dfrac{\pi }{2}$
Trong đó:
$\omega =\dfrac{1}{\sqrt{LC}}=2{\pi}f$ là tần số góc riêng
${{I}_{0}}=\omega {{q}_{0}}=\dfrac{{{q}_{0}}}{\sqrt{LC}}=\omega C{{U}_{0}}={{U}_{0}}\sqrt{\dfrac{C}{L}}$
${{U}_{0}}=\dfrac{{{q}_{0}}}{C}=\dfrac{{{I}_{0}}}{\omega C}=\omega L{{I}_{0}}={{I}_{0}}\sqrt{\dfrac{L}{C}}$
Sự biến thiên điều hòa theo thời gian của điện tích q của một bản tụ điện và cường độ dòng điện I ( hoặc cường độ điện trường $\overrightarrow{E}$ và cảm ứng từ $\overrightarrow{B}$) trong mạch dao động được gọi là dao động điện từ tự do.
Bài tập tự luyện có đáp án
Câu 1: Một mạch dao động LC lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại của một bản tụ điện có độ lớn là ${10^{ - 8}}C$ và cường độ dòng điện cực đại qua cuộn cảm thuần là 62,8 mA. Tần số dao động điện từ tự do của mạch là
- A
- B
- C
- D
Ta có: ${{\rm{I}}_0} = \omega {q_0} \to \omega = \dfrac{{{{\rm{I}}_0}}}{{{q_0}}} = \dfrac{{62,{{8.10}^{ - 3}}}}{{{{10}^{ - 8}}}} = 6,{28.10^6}ra{\rm{d}}/s \to f = {10^3}kHz$
Câu 2: Một mạch dao động LC lí tưởng gồm tụ điện có điện dung 18 nF và cuộn cảm thuần có độ tự cảm 6 $\mu H$. Trong mạch đang có dao động điện từ với hiệu điện thế cực đại giữa hai bản tụ điện là 2,4 V. Cường độ dòng điện hiệu dụng trong mạch có giá trị là
Một mạch dao động LC lí tưởng gồm tụ điện có điện dung 18 nF và cuộn cảm thuần có độ tự cảm 6 $\mu H$. Trong mạch đang có dao động điện từ với hiệu điện thế cực đại giữa hai bản tụ điện là 2,4 V. Cường độ dòng điện hiệu dụng trong mạch có giá trị là
- A
- B
- C
- D
\({{\rm{I}}_0} = \omega {q_0} = \dfrac{1}{{\sqrt {LC} }}.C{U_0} \Rightarrow {I_0} = {U_0}\sqrt {\dfrac{C}{L}} = 2,4\sqrt {\dfrac{{{{18.10}^{ - 9}}}}{{{{6.10}^{ - 6}}}}} \approx 0,13145{\rm{ }}A \to I = \dfrac{{{I_0}}}{{\sqrt 2 }} = 0,09295\left( A \right) = 92,95{\rm{ }}mA.\)
Câu 3: Trong một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do với điện tích trên một bản của tụ điện có biểu thức là $q={{3.10}^{-6}}c\text{os}\left( 2000t \right)\text{ }C$. Biểu thức của cường độ dòng điện trong mạch là
- A
- B
- C
- D
Giá trị cực đại và pha ban đầu của dòng điện i là:
$\left\{ \begin{array}{l}{I_0} = \omega {q_0} = q = {3.10^{ - 6}}.2000 = {6.10^{ - 3}}A = 6{\rm{ mA}}{\rm{.}}\\{\varphi _i} = {\varphi _q} + \dfrac{\pi }{2} = \dfrac{\pi }{2}\end{array} \right.{\rm{ }}i = 6\cos \left( {2000t + \dfrac{\pi }{2}} \right)mA.$
Câu 4: Một mạch dao động lí tưởng đang có dao động điện từ tự do. Cường độ dòng điện tức thời trong một mạch dao động là i = 0,05cos(100πt) A. Lấy $π^2 = 10$. Biểu thức điện tích của một bản trên tụ điện là
- A
- B
- C
- D
Giá trị cực đại và pha ban đầu của điện tích q là:
\(\left\{ \begin{array}{l}{q_o} = \dfrac{{{I_o}}}{\omega } = \dfrac{{0,05}}{{100\pi }} = \dfrac{{{{5.10}^{ - 4}}}}{\pi }C\\{\varphi _q} = {\varphi _i} - \dfrac{\pi }{2} = - \dfrac{\pi }{2}\end{array} \right.{\rm{ }}q = \dfrac{{{{5.10}^{ - 4}}}}{\pi }\cos \left( {100\pi t - \dfrac{\pi }{2}} \right)C.\)
Câu 5: Cường độ dòng điện tức thời trong mạch dao động LC có dạng i = 0,05sin(2000t) A. Tần số góc dao động của mạch là
- A
- B
- C
- D
Cường độ dòng điện tức thời trong mạch dao động LC có dạng $i = I_0sin(ωt) A$
Câu 6: Mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Trong mạch đang có dao động điện từ tự do. Gọi $U_0$ là hiệu điện thế cực đại giữa hai bản tụ và $I_0$ là cường độ dòng điện cực đại trong mạch. Hệ thức đúng là
- A
- B
- C
- D
Ta có: \({{\rm{I}}_0} = \omega {q_0} = \dfrac{1}{{\sqrt {LC} }}.C{U_0} \Rightarrow {{\rm{I}}_0} = {U_0}\sqrt {\dfrac{C}{L}} \)
Câu 7: Mạch dao động LC gồm tụ điện có điện dung 16 nF và cuộn cảm có độ tự cảm 25 mH. Tần số góc dao động của mạch là:
- A
- B
- C
- D
Ta có: $\omega = \dfrac{1}{{\sqrt {LC} }} = \dfrac{1}{{\sqrt {{{25.10}^{ - 3}}{{.16.10}^{ - 9}}} }} = {5.10^4}\left( {H{\rm{z}}} \right)$
Câu 8: Một mạch dao động LC lí tưởng, gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Trong mạch có dao động điện từ tự do. Gọi $U_0, I_0$ lần lượt là hiệu điện thế cực đại giữa hai đầu tụ điện và cường độ dòng điện cực đại trong mạch thì
- A
- B
- C
- D
Ta có: ${{\rm{I}}_0} = \omega {q_0} = \dfrac{1}{{\sqrt {LC} }}.C{U_0} \Rightarrow {U_0} = {\rm{ }}{{\rm{I}}_0}\sqrt {\dfrac{L}{C}} $
Câu 9: Một mạch dao động điện từ lí tưởng gồm một tụ điện có điện dung 0,125 μF và một cuộn cảm có độ tự cảm 50 μH. Cường độ dòng điện cực đại trong mạch là 0,15 A. Hiệu điện thế cực đại giữa hai bản tụ điện là
- A
- B
- C
- D
Ta có: \({{\rm{I}}_0} = \omega {q_0} = \dfrac{1}{{\sqrt {LC} }}.C{U_0} \Rightarrow {U_0} = {\rm{ }}{{\rm{I}}_0}\sqrt {\dfrac{L}{C}} = 0,15.\sqrt {\dfrac{{{{50.10}^{ - 6}}}}{{0,{{125.10}^{ - 6}}}}} = 3\left( V \right)\)
Câu 10: Trong một mạch dao động điện từ lí tưởng đang có dao động điện từ tự do với điện tích trên một bản của tụ điện có biểu thức là $ q={{3.10}^{-6}}c\text{os}\left( 2000t \right)\text{ }C $ . Biểu thức của cường độ dòng điện trong mạch là
- A
- B
- C
- D
Giá trị cực đại và pha ban đầu của dòng điện i là:
$ \begin{array}{l} \left\{ \begin{array}{l} {{I}_{0}}=\omega {{q}_{0}}=q={{3.10}^{-6}}.2000=6\text{ mA}\text{.} \\ {{\varphi }_{i}}={{\varphi }_{q}}+\dfrac{\pi }{2}=\dfrac{\pi }{2} \end{array} \right.\text{ } \\ \Rightarrow i=6\cos \left( 2000t+\dfrac{\pi }{2} \right)mA. \end{array} $
Câu 11: Mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Trong mạch đang có dao động điện từ tự do. Gọi $q_0$ là điện tích cực đại trên tụ và $I_0$ là cường độ dòng điện cực đại trong mạch. Hệ thức đúng là
- A
- B
- C
- D
Ta có: \({{\rm{I}}_0} = \omega {q_0} \Leftrightarrow {{\rm{I}}_0} = \dfrac{{{q_0}}}{{\sqrt {LC} }}\)
Câu 12: Một mạch dao động LC lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại của một bản tụ điện có độ lớn là $0,{16.10^{-11}}C$ và cường độ dòng điện cực đại qua cuộn cảm thuần là 1 mA. Tần số góc của mạch dao động LC này là
- A
- B
- C
- D
Ta có: \({{\rm{I}}_0} = \omega {q_0} \Rightarrow \omega = \dfrac{{{{\rm{I}}_0}}}{{{q_0}}} = \dfrac{{{{10}^{ - 3}}}}{{0,{{16.10}^{ - 11}}}} = {625.10^6}\left( {ra{\rm{d}}/s} \right)\)
Câu 13: Một mạch dao động LC lí tưởng đang có dao động điện từ tự do với chu kì T. Biết điện tích cực đại của một bản tụ điện có độ lớn là $10^{–8} C$ và cường độ dòng điện cực đại qua cuộn cảm là 62,8 mA. Giá trị của T là
- A
- B
- C
- D
Ta có: ${{\rm{I}}_0} = \omega {q_0} = \dfrac{{2\pi }}{T}.{q_0} \to T = \dfrac{{2\pi .{q_0}}}{{{{\rm{I}}_0}}} = \dfrac{{2\pi {{.10}^{ - 8}}}}{{62,{{8.10}^{ - 3}}}} = {10^{ - 6}}\left( s \right) = 1\left( {\mu s} \right)$
Câu 14: Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Trong mạch đang có dao động điện từ tự do. Biết điện tích cực đại trên một bản tụ điện là $q_0$ và cường độ dòng điện cực đại trong mạch là $I_0$. Tần số dao động tính theo công thức
- A
- B
- C
- D
Ta có: \({{\rm{I}}_0} = \omega {q_0} \Leftrightarrow {{\rm{I}}_0} = 2\pi f{q_0} \Rightarrow f = \dfrac{{{{\rm{I}}_0}}}{{2\pi {q_0}}}\)
Câu 15: Một mạch dao động điện từ LC lí tưởng đang thực hiện dao động điện từ tự do. Điện tích cực đại trên một bản tụ là $2.10^{-6} C$, cường độ dòng điện cực đại trong mạch là 0,1π A. Chu kì dao động điện từ tự do trong mạch bằng
- A
- B
- C
- D
Ta có: ${{\rm{I}}_0} = \omega {q_0} = \dfrac{{2\pi }}{T}.{q_0} \to T = \dfrac{{2\pi .{q_0}}}{{{{\rm{I}}_0}}} = \dfrac{{2\pi {{.2.10}^{ - 6}}}}{{0,1\pi }} = {4.10^{ - 5}}\left( s \right)$
Câu 16: Một mạch dao động điện từ lí tưởng, đang có dao động điện từ tự do. Biểu thức cường độ dòng điện trong mạch là $i = 0,04cos(2.10^7t) (A)$. Điện tích cực đại của tụ điện là
- A
- B
- C
- D
Ta có: \({{\rm{I}}_0} = \omega {Q_0} \Leftrightarrow {Q_0} = \dfrac{{{{\rm{I}}_0}}}{\omega } = \dfrac{{0,04}}{{{{2.10}^7}}} = {2.10^{ - 9}}\left( C \right)\)
Câu 17: Trong mạch dao động LC lí tưởng đang có dao động điện từ tự do, điện tích của một bản tụ điện và cường độ dòng điện qua cuộn cảm thuần biến thiên điều hòa theo thời gian
- A
- B
- C
- D
Phương trình điện tích: $q = q_0cos(ωt + φ)$
Phương trình dòng điện: $i = I_0cos(ωt + φ + π/2)$
⟹ i và q biến thiên điều hòa cùng tần số
Câu 18: Một mạch dao động LC gồm cuộn cảm có độ tự cảm L và tụ điện có điện dung 0,5 μF. Tần số góc dao động của mạch là 2000 rad/s. Giá trị L là
- A
- B
- C
- D
Ta có: \(\omega = \dfrac{1}{{\sqrt {LC} }} \Leftrightarrow 2000 = \dfrac{1}{{\sqrt {L.0,{{5.10}^{ - 6}}} }} \Rightarrow L = 0,5\left( H \right)\)
Câu 19: Mạch dao động điện từ LC lí tưởng đang hoạt động, biểu thức điện tích của một bản tụ điện là $ q={{2.10}^{-9}}cos({{2.10}^{7}}t+\dfrac{\pi }{4})\left( C \right) $ . Cường độ dòng điện cực đại trong mạch là
- A
- B
- C
- D
$ {{\text{I}}_{0}}=\omega {{q}_{0}}={{2.10}^{7}}{{.2.10}^{-9}}=0,04\left( \text{A} \right)=40\text{ }\left( mA \right) $
Câu 20: Mạch dao động điện từ LC lí tưởng đang hoạt động. Điện tích của một bản tụ điện
- A
- B
- C
- D
Điện tích của một bản tụ điện biến thiên điều hòa theo thời gian theo phương trình: $q = q_0cos(ωt + φ)$
Câu 21: Mạch dao động điện từ LC lí tưởng đang hoạt động, biểu thức điện tích của một bản tụ điện là $q = 2.10^{−9}cos(2.10^7t +$$\dfrac{\pi }{4}$ ) (C). Cường độ dòng điện cực đại trong mạch là
- A
- B
- C
- D
Ta có: ${{\rm{I}}_0} = \omega {q_0} = {2.10^7}{.2.10^{ - 9}} = 0,04\left( {\rm{A}} \right) = 40{\rm{ }}\left( {mA} \right)$
Câu 22: Mạch dao động gồm cuộn thuần cảm và tụ điện có điện dung 10 μF. Trong mạch có dao động điện từ tự do. Khi điện áp giữa hai bản tụ là 8 V thì điện tích trên tụ điện là
- A
- B
- C
- D
Ta có: \(q=C.u=10.8=80\text{ }\mu C\)
Câu 23: Mạch dao động điện từ điều hoà có cấu tạo gồm
- A
- B
- C
- D
Mạch dao động điện từ điều hoà có cấu tạo gồm tụ điện và cuộn cảm mắc thành mạch kín.
Câu 24: Phương trình dao động của điện tích trong mạch dao động LC là $ q={{q}_{0}}\cos (\omega t+\varphi ) $ . Biểu thức của hiệu điện thế giữa hai bản tụ điện là
- A
- B
- C
- D
$ q={{q}_{0}}\cos (\omega t+\varphi )\Rightarrow u={{U}_{0}}\cos (\omega t+\varphi )=\dfrac{{{q}_{0}}}{C}\cos (\omega t+\varphi ) $
Câu 25: Trong một mạch dao động lí tưởng đang có dao động điện từ tự do. Biết điện tích cực đại trên một bản tụ điện là $4.10^{−8} C$ và cường độ dòng điện cực đại trong mạch là 10mA. Tần số dao động điện từ trong mạch là
- A
- B
- C
- D
Ta có: ${{\rm{I}}_0} = \omega {q_0} = 2\pi f.{q_0} \to f = \dfrac{{{{\rm{I}}_0}}}{{2\pi .{q_0}}} = \dfrac{{{{10.10}^{ - 3}}}}{{2\pi {{.4.10}^{ - 8}}}} = 39,{8.10^3}\left( {kH{\rm{z}}} \right)$
Câu 26: Một mạch dao động gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Tần số góc riêng của mạch dao động này là
Một mạch dao động gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Tần số góc riêng của mạch dao động này là
- A
- B
- C
- D
$\omega =\dfrac{1}{\sqrt{LC}}.$
Câu 27: Cường độ dòng điện tức thời trong mạch dao động LC có dạng $i = I_0cos(2000t) A$. Tụ điện trong mạch có điện dung $5 μF$. Độ tự cảm của cuộn cảm là
- A
- B
- C
- D
Ta có: \(\omega = \dfrac{1}{{\sqrt {LC} }} \Rightarrow L = \dfrac{1}{{{\omega ^2}.C}} = \dfrac{1}{{{{2000}^2}{{.5.10}^{ - 6}}}} = 0,05\left( H \right) = 50\left( {mH} \right)\)
Câu 28: Một mạch dao động lí tưởng đang có dao động điện từ tự do. Cường độ dòng điện tức thời trong một mạch dao động là $ i=0,05cos\left( 100\pi t \right)A $ . Lấy $ {{\pi }^{2}}=10 $ . Biểu thức điện tích của một bản trên tụ điện là
- A
- B
- C
- D
Giá trị cực đại và pha ban đầu của điện tích q là:
$ \left\{ \begin{array}{l} {{q}_{o}}=\dfrac{{{I}_{o}}}{\omega }=\dfrac{0,05}{100\pi }=\dfrac{{{5.10}^{-4}}}{\pi }C \\ {{\varphi }_{q}}={{\varphi }_{i}}-\dfrac{\pi }{2}=-\dfrac{\pi }{2} \end{array} \right.\text{ }\Rightarrow q=\dfrac{{{5.10}^{-4}}}{\pi }\cos \left( 100\pi t-\dfrac{\pi }{2} \right)C. $
Câu 29: Một mạch dao động điện từ lí tưởng gồm cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C. Tần số góc dao động riêng của mạch là
- A
- B
- C
- D
Tần số góc dao động riêng của mạch là: $\omega =\dfrac{1}{\sqrt{LC}}.$
Câu 30: Phương trình dao động của điện tích trong mạch dao động LC là \(q={{q}_{0}}\cos (\omega t+\varphi )\). Biểu thức của hiệu điện thế giữa hai bản tụ điện là
- A
- B
- C
- D
Ta có: \(u=\dfrac{q}{C}=\dfrac{{{q}_{0}}}{C}\cos (\omega t+\varphi )\)
Câu 31: Trong mạch dao động LC lí tưởng đang có dao động điện từ tự do, cường độ dòng điện trong mạch và hiệu điện thế giữa hai bản tụ điện lệch pha nhau một góc bằng
- A
- B
- C
- D
Phương trình hiệu điện thế giữa hai bản tụ: $u = U_0cos(ωt + φ)$
Phương trình dòng điện: $i = I_0cos(ωt + φ + π/2)$
⟹ i nhanh pha hơn u một góc π/2
Câu 32: Biểu thức của cường độ dòng điện trong mạch dao động LC là \(i={{I}_{0}}\cos (\omega t+\varphi )\). Biểu thức của điện tích của một bản tụ điện là
- A
- B
- C
- D
\({{Q}_{0}}=\dfrac{{{I}_{0}}}{\omega }\)
q chậm pha hơn i một góc π/2 nên
\(q=\dfrac{{{I}_{0}}}{\omega }\cos \left( \omega t+\varphi -\dfrac{\pi }{2} \right)\)
Câu 33: Một mạch dao động LC lí tưởng đang có dao động điện từ tự do với điện tích cực đại của tụ điện là $Q_0$ và cường độ dòng điện cực đại trong mạch là $I_0$. Dao động điện từ tự do trong mạch có chu kì là
- A
- B
- C
- D
Ta có: \({{\rm{I}}_0} = \omega {Q_0} \Leftrightarrow {{\rm{I}}_0} = \dfrac{{2\pi }}{T}{Q_0} \Rightarrow T = \dfrac{{2\pi {Q_0}}}{{{{\rm{I}}_0}}}\)