Cắt lò xo
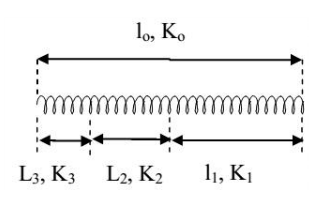
Lý thuyết về Cắt lò xo
Công thức tính độ cứng của lò xo:
$k=E.\dfrac{S}{l}\Leftrightarrow k.l=E.S\left( 1 \right)$
Trong đó: k là độ cứng của lò xo (N/m)
l là chiều dài của lò xo (m)
E là suất đàn hồi hay suất Young (Pa)
S là tiết diện của lò xo
Với một lò xo xác định thì suất đàn hồi và tiết diện của lò xo không đổi nên $E.S=h/s$
Từ (1)$\Rightarrow k.l=h/s$
Một lò xo có độ cứng k, chiều dài l được cắt thành các lò xo có độ cứng ${{k}_{1}},{{k}_{2}},$ ${{k}_{3}}$… và chiều dài tương ứng là ${{l}_{1}},{{l}_{2}},$${{l}_{3}}$ … thì có:
$kl={{k}_{1}}{{l}_{1}}={{k}_{2}}{{l}_{2}}=\ldots $
Bài tập tự luyện có đáp án
Câu 1: Một con lắc lò xo có chiều dài tự nhiên là $l_0$, độ cứng k, vật nhỏ khối lượng m , có chu kì 2s. Nếu cắt bớt lò xo đi 20 cm rồi cho con lắc dao động điều hòa thì chu kì của nó là $\dfrac{4\sqrt{5}}{5}$ (s). Hỏi nếu cắt bớt lò xo đi 40 cm rồi cho con lắc dao động điều hòa thì chu kì của nó là bao nhiêu ?
- A
- B
- C
- D
+ Độ dài lò xo khi cắt bớt 20 cm là: $ℓ_1 = ℓ_0– 20 \Rightarrow$ $\dfrac{{{T}_{1}}}{{{T}_{0}}}=\sqrt{\dfrac{{{k}_{0}}}{{{k}_{1}}}}=\sqrt{\dfrac{{{\ell }_{1}}}{{{\ell }_{0}}}}\Leftrightarrow \dfrac{\dfrac{4\sqrt{5}}{5}}{2}=\sqrt{\dfrac{{{\ell }_{0}}-20}{{{\ell }_{0}}}}\Rightarrow {{\ell }_{0}}=100cm$
+ Độ dài lò xo khi cắt bớt 40 cm là: $ℓ_2 = ℓ_0– 40 = 60 cm$
$\Rightarrow$ $\dfrac{{{T}_{2}}}{{{T}_{0}}}=\sqrt{\dfrac{{{k}_{0}}}{{{k}_{2}}}}=\sqrt{\dfrac{{{\ell }_{2}}}{{{\ell }_{0}}}}=\sqrt{\dfrac{60}{100}}\Rightarrow {{T}_{2}}=1,55\text{s}$