Bài toán quãng đường trong dao động điều hòa
Lý thuyết về Bài toán quãng đường trong dao động điều hòa
1. Quãng đường vật đi được trong nT
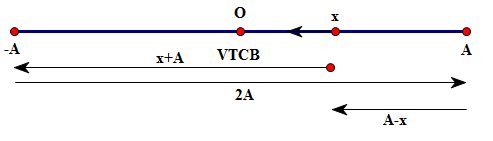
Xét vật dao động điều hòa bắt đầu dao động từ điểm có li độ x và chuyển động theo chiều âm. Trong một chu kì quãng đường vật đi được là: S=(x+A)+2A+(A-x)=4A
Quãng đường đi được trong thời gian nT là ${{S}_{}}=4nA$
2. Quãng đường lớn nhất
t=nT+T/2+$\Delta t$
Trong nT vật đi được quãng đường là 4nA, Trong T/2 vật luôn đi được quãng đường là 2A.
Trong khoảng thời gian $\Delta t$ vật quét được góc: $\Delta \varphi =\omega .\Delta t$
Vật đi được quãng đường lớn nhất trong một khoảng thời gian cho trước thì vật phải có tốc độ lớn nhất .Mà tốc độ lớn nhất của vật ở VTCB nên vật muốn có quãng đường lớn nhất vật phải đi quanh VTCB.
Quãng đường lớn nhất khi vật đi từ M1 đến M2 đối xứng qua trục sin
$\begin{align} & {{M}_{1}}{{M}_{2}}={{P}_{1}}{{P}_{2}}=2O{{P}_{1}} \\ & O{{P}_{1}}\text{=A}\sin \frac{\Delta \varphi }{2} \\ \end{align}$
${{M}_{1}}{{M}_{2}}=$${{S}_{M\text{ax}}}=2\text{A}\sin \dfrac{\Delta \varphi }{2}$$\left( \Delta \varphi \le \frac{\pi }{2} \right)$
3. Quãng đường nhỏ nhất
t=nT+T/2+$\Delta t$
Trong nT vật đi được quãng đường là 4nA, Trong T/2 vật luôn đi được quãng đường là 2A.
Trong khoảng thời gian $\Delta t$ vật quét được góc: $\Delta \varphi =\omega .\Delta t$
Vật đi được quãng đường nhỏ nhất trong một khoảng thời gian cho trước thì vật phải có tốc độ nhỏ nhất .Mà tốc độ nhỏ nhất của vật ở biên nên vật muốn có quãng đường nhỏ nhất vật phải đi quanh VT biên.
Quãng đường nhỏ nhất khi vật đi từ M1 đến M2 đối xứng qua trục cos
${{S}_{\min }}=2AP$
$AP=A-A\cos \dfrac{\Delta \varphi }{2}$$\Rightarrow {{S}_{Min}}=2A(1-c\text{os}\dfrac{\Delta \varphi }{2})$$\left( \Delta \varphi \le \dfrac{\pi }{2} \right)$
4. Quãng đường đi được trong nửa chu kì
Trong $\frac{T}{2}$ chu kì vật dao động điều hòa thực hiện được $\frac{1}{2}$ dao động toàn phần nên vật chuyển động tròn đều tương ứng chuyển động được $\frac{1}{2}$ vòng. Vật chuyển động tròn đều đi từ ${{M}_{1}}\to {{M}_{2}}$ thì hình chiếu tương ứng của nó ( vật dao động điều hòa) đi từ ${{N}_{1}}\to {{N}_{2}}$ )
Ta có: $O{{N}_{1}}=O{{N}_{2}}$ ( 2 cạnh tương ứng)
$\Rightarrow $ điểm ${{N}_{1}}$ có li độ x và điểm ${{N}_{2}}$ có li độ -x
Quãng đường đi được của vật dao động điều hòa trong $\frac{T}{2}$ là
S=(A-x)+A-x
Từ hình vẽ ta thấy. Cứ sau ( trước) $\frac{T}{2}$ vận tốc và chu kì đổi dấu ( v>0 sau (trước) $\frac{T}{2}$ v<0; x>0 sau (trước) $\frac{T}{2}$ x<0 và ngược lại)
Bài tập tự luyện có đáp án
Câu 1: Một vật dao động điều hòa với biên độ A và chu kì T, mốc thời gian t = 0 vật đang ở vị trí biên, phát biểu nào sau đây là không đúng?
- A
- B
- C
- D
Ban đầu vật ở vị trí biên nên sau $ \dfrac{T}{4} $ vật đi được quãng đường A, sau $ \dfrac{T}{2} $ vật đi được quãng đường 2A, Sau $ T $ vật đi được quãng đường 4A
Câu 2: Một chất điểm dao động điều hòa với biên độ A, quãng đường vật đi trong một nửa chu kì
- A
- B
- C
- D
Quãng đường vật đi được trong một nửa chu kì là 2A
Câu 3: Một chất điểm dao động điều hòa với biên độ A, ban đầu vật ở vị trí cân bằng đi theo chiều âm quãng đường mà vật đi trong $ \dfrac{3}{4} $ chu kì đầu tiên là
- A
- B
- C
- D
$ \Delta t=\dfrac{3T}{4}=\dfrac{T}{4}+\dfrac{T}{2} $
Gọi $ \varphi $ là góc mà vật quét được khi vật đi được trong khoảng thời gian $ \dfrac{T}{4} $
$ \varphi =\dfrac{2\pi }{T}.\dfrac{T}{4}=\dfrac{\pi }{2} $
Mà ban đầu vật ở vị trí cân bằng đi theo chiều âm nên khi đó quãng đường vật đi trong $ \dfrac{T}{4} $ là A, quãng đường vật đi được trong $ \dfrac{T}{2} $ là 2A, vậy quãng đường đi được $ \dfrac{3T}{4} $ là: A+2A=3A
Câu 4: Một chất điểm dao động điều hòa với biên độ A, ban đầu vật ở vị trí biên âm, quãng đường mà vật đi trong $ \dfrac{3}{4} $ chu kì đầu tiên là
- A
- B
- C
- D
$ \Delta t=\dfrac{3T}{4}=\dfrac{T}{4}+\dfrac{T}{2} $
Gọi $ \varphi $ là góc mà vật quét được khi vật đi được trong khoảng thời gian $ \dfrac{T}{4} $
$ \varphi =\dfrac{2\pi }{T}.\dfrac{T}{4}=\dfrac{\pi }{2} $
Mà ban đầu vật ở biên âm nên quãng đường vật đi trong $ \dfrac{T}{4} $ là A, quãng đường vật đi được trong $ \dfrac{T}{2} $ là 2A, vậy quãng đường đi được $ \dfrac{3T}{4} $ là: A+2A=3A
Câu 5: Một chất điểm dao động điều hòa với biên độ A, ban đầu vật ở vị trí cân bằng đi theo chiều dương, quãng đường mà vật đi trong $ \dfrac{1}{4} $ chu kì đầu tiên là
- A
- B
- C
- D
Gọi $ \varphi $ là góc mà vật quét được khi vật đi được trong khoảng thời gian $ \dfrac{T}{4} $
$ \varphi =\dfrac{2\pi }{T}.\dfrac{T}{4}=\dfrac{\pi }{2} $
Mà ban đầu vật ở vị trí cân bằng đi theo chiều dương nên khi đó vật đến biên dương , vậy quãng đường vật đi trong $ \dfrac{T}{4} $ là A
Câu 6: Một chất điểm dao động điều hòa với biên độ A, quãng đường vật đi trong n chu kì
- A
- B
- C
- D
Quãng đường vật đi được trong 1 chu kì là 4A, vậy quãng đường vật đi được trong nT chu kì là: 4nA
Câu 7: Một chất điểm dao động điều hòa với biên độ A, ban đầu vật ở vị trí biên dương quãng đường mà vật đi trong $ \dfrac{1}{4} $ chu kì đầu tiên là
- A
- B
- C
- D
Gọi $ \varphi $ là góc mà vật quét được khi vật đi được trong khoảng thời gian $ \dfrac{T}{4} $
$ \varphi =\dfrac{2\pi }{T}.\dfrac{T}{4}=\dfrac{\pi }{2} $
Mà ban đầu vật ở vị trí biên dương nên khi đó vật đến vị trí cân bằng, vậy quãng đường vật đi trong $ \dfrac{T}{4} $ là A
Câu 8: Một vật dao động điều hòa với biên độ A và chu kì T, quãng đường nhỏ nhất mà vật đi được trong khoảng thời gian $ \dfrac{T}{3} $
- A
- B
- C
- D
Trong khoảng thời gian $ \Delta t=\dfrac{T}{3} $ quãng đường nhỏ nhất vật đi được là:
$ S=2\text{A}(1-c\text{os}\dfrac{\Delta \varphi }{2})=2\text{A}\left( 1-c\text{os}\dfrac{\dfrac{2\pi }{T}.\dfrac{T}{3}}{2} \right)=\text{A} $
Câu 9: Một chất điểm dao động điều hòa với biên độ A, ban đầu vật ở vị trí cân bằng đi theo chiều âm, quãng đường mà vật đi trong $ \dfrac{1}{4} $ chu kì đầu tiên là
- A
- B
- C
- D
Gọi $ \varphi $ là góc mà vật quét được khi vật đi được trong khoảng thời gian $ \dfrac{T}{4} $
$ \varphi =\dfrac{2\pi }{T}.\dfrac{T}{4}=\dfrac{\pi }{2} $
Mà ban đầu vật ở vị trí cân bằng đi theo chiều âm nên khi đó vật đến biên âm , vậy quãng đường vật đi trong $ \dfrac{T}{4} $ là A .
Câu 10: Một chất điểm dao động điều hòa với biên độ A, ban đầu vật ở vị trí biên âm quãng đường mà vật đi trong $ \dfrac{1}{4} $ chu kì đầu tiên là
- A
- B
- C
- D
Gọi $ \varphi $ là góc mà vật quét được khi vật đi được trong khoảng thời gian $ \dfrac{T}{4} $
$ \varphi =\dfrac{2\pi }{T}.\dfrac{T}{4}=\dfrac{\pi }{2} $
Mà ban đầu vật ở trí biên âm nên khi đó vật đến vị trí cân bằng, vậy quãng đường vật đi trong $ \dfrac{T}{4} $ là A
Câu 11: Một chất điểm dao động điều hòa với biên độ A. Quãng đường mà chất điểm đi được trong một chu kì là
- A
- B
- C
- D
Quãng đường mà chất điểm đi được trong một chu kì là 4A.
Xem thêm các bài tiếp theo bên dưới