Từ thông
Lý thuyết về Từ thông
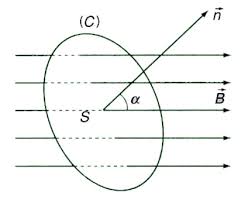
Giả sử một đờng cong phẳng kín (C) là chu vi giới hạn một mặt có diện tích S. Mặt đó được đặt trong một từ trường đều →B.
Trên đường vuông góc với mặt S, ta vẽ vecto →n có độ dài bằng đơn vị theo một hướng xác định ( tùy ý chọn), →n được gọi là vecto pháp tuyến dương. Gọi α là góc tạo bởi →n và →B
Định nghĩa từ thông qua mặt S là đại lượng, kí hiệu ϕ cho bởi: ϕ=BScosα
Đặc điểm: Từ thông là một đại lượng đại số.
+ Khi α nhọn (cosα>0) thì ϕ>0
+ Khi α tù (cosα<0)thì ϕ<0.
+ Đặc biệt khi α=90o(cosα=0) thì ϕ=0.
Nói cách khác, khi các đường sức từ song song với mặt S thì từ thông qua S bằng 0.
Trường hợp riêng, khi α=0 thì: ϕ=BS
Bài tập tự luyện có đáp án
Câu 1: Mặt bán cầu đường kính 2R đặt trong một từ trường đều có cảm ứng từ →B song song với trục đối xứng của mặt bán cầu. Từ thông qua mạch bán cầu là:
- A
- B
- C
- D
Từ thông qua mặt bán cầu là:
Φ=B.S=B.π.R2
Câu 2: Giá trị tuyệt đối của từ thông qua diện tích S đặt vuông góc với cảm ứng từ →B
- A
- B
- C
- D
Giá trị tuyệt đối của từ thông qua diện tích S đặt vuông góc với cảm ứng từ →B tỉ lệ với số đường sức từ qua diện tích S
Câu 3: Tìm câu đúng?
- A
- B
- C
- D
+ Câu trả lời đúng là: →n gọi là vectơ đơn vị pháp tuyến của mặt S thì →nvuông góc với mặt S và có độ dài bằng đơn vị.
+ Từ thông là đại lượng vô hướng được xác định theo: Φ=BScosα, đơn vị là Wb.
Câu 4: Phát biểu nào sau đây không đúng về từ thông.
- A
- B
- C
- D
Từ thông là đại lượng vô hướng
Câu 5: Một khung dây có diện tích S đặt trong từ trường đều có cảm ứng từ B sao cho mặt phẳng khung dây vuông góc với đường sức từ. Gọi ϕ là từ thông gửi qua khung dây. Độ lớn của ϕ bằng:
- A
- B
- C
- D
Áp dụng công thức tính từ thông qua vòng dây ϕ=NBScosα
Vì có 1 khung dây nên N = 1; cảm ứng từ B sao cho mặt phẳng khung dây vuông góc với đường sức từ ⇒cosφ=1 . Vậy từ thông gửi qua khung dây là ϕ=B.S
Câu 6: Cho một khung dây có diện tích S đặt trong từ trường đều có cảm ứng từ B, α là góc hợp bởi vectơ pháp tuyến của khung và vectơ cảm ứng từ B. Từ thông được xác định bởi biểu thức nào sau đây?
- A
- B
- C
- D
Từ thông được xác định bởi biểu thức: Φ=B.S.cosα
Trong đó S diện tích khung dây ( m2 )
B là cảm ứng từ (T)
α là góc hợp bởi vectơ pháp tuyến của khung và vectơ cảm ứng từ B
Câu 7: Từ thông qua mỗi mặt S có độ lớn
- A
- B
- C
- D
Φ=B.S.cos(α)
Nên từ thông qua mỗi mặt S có độ lớn tỉ lệ với số đường sức từ qua S.
Câu 8: Đơn vị của từ thông là
- A
- B
- C
- D
Đơn vị của từ thông là vêbe (Wb).
Câu 9: Xét mạch kín (C) định hướng đặt trong từ trường, từ thông qua các mặt bất kì có cùng (C)
- A
- B
- C
- D
Mạch kín (C) định hướng đặt trong từ trường, từ thông qua các mặt bất kì có cùng (C) thì chu vi đều bằng nhau.
Câu 10: Ngoài đơn vị là Vêbe(WB) từ thông có đơn vị là:
- A
- B
- C
- D
Ta có: Φ=B.S.cosα mà B có đơn vị là Tesla (T), S có đơn vị là mét bình phương ( m2 )
⇒1Wb=1T.1m2=T.m2
Câu 11: Đơn vị của từ thông
- A
- B
- C
- D
Đơn vị của từ thông là Wb ( Vêbe)
Câu 12: Định luật Len-xơ cho phép ta xác định
- A
- B
- C
- D
Định luật Len-xơ cho phép ta xác định chiều dòng điện cảm ứng xuất hiện trong mạch.
Định luật phát biểu: Dòng điện cảm ứng có chiều sao cho từ trường do nó dinh ra có tác dụng chống lại nguyên nhân đã sinh ra nó.
Câu 13: Cho khung dây hình tròn? Biểu thức nào dưới đây biểu diễn một đại lượng có đơn vị là vêbe (Wb)
- A
- B
- C
- D
Vêbe là đơn vị của từ thông mà biểu thức xác định từ thông:
Φ=B.S.cosα
mặt khác πr2 là diện tích hình tròn nên Φ=B.πr2.cosα trường hợp cosα=1 ⇒Φ=Bπr2
Câu 14: Chọn câu đúng. Từ thông đi qua vòng dây trong từ trường →B không phụ thuộc vào
- A
- B
- C
- D
Từ thông đi qua vòng dây trong từ trường →B không phụ thuộc vào hình dạng của vòng dây do ϕ=B.S.cosα.
Câu 15: Phát biểu nào sau đây không đúng khi nói về từ thông qua mặt S?
- A
- B
- C
- D
Từ thông qua mặt S phụ thuộc diện tích mặt S nên sẽ phu thuộc vào số đo chu vi của S.
Xem thêm các bài tiếp theo bên dưới