Điều kiện để điện tích cân bằng
Lý thuyết về Điều kiện để điện tích cân bằng
1. Hai điện tích:
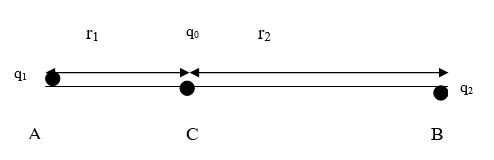
Hai điện tích q1;q2q1;q2 đặt tại hai điểm A và B, hãy xác định điểm C đặt điện tích qoqođể qoqo cân bằng:
- Điều kiện cân bằng của điện tích qoqo:
→Fo=→F10+→F20=→0⃗Fo=⃗F10+⃗F20=⃗0
⇔⇔ →F10=−→F20⃗F10=−⃗F20
⇒⇒ {→F10↑↓→F20F10=F20 (1)(2)
+ Trường hợp 1: q1;q2 cùng dấu:
Từ (1) ⇒ C thuộc đoạn thẳng AB: AC + BC = AB (*)
Ta có: |q1|r21=|q2|r22
+ Trường hợp 2: q1;q2 trái dấu:
Từ (1) ⇒ C thuộc đường thẳng AB: |AC−BC|=AB(* ’)
Ta cũng vẫn có: |q1|r21=|q2|r22
- Từ (2) ⇒ |q2|.AC2−|q1|.BC2=0 (**)
- Giải hệ hai pt (*) và (**) hoặc (* ’) và (**) để tìm AC và BC.
* Nhận xét:
- Biểu thức (**) không chứa qo nên vị trí của điểm C cần xác định không phụ thuộc vào dấu và độ lớn của qo.
-Vị trí cân bằng nếu hai điện tích trái dấu thì điểm cân bằng nằm ngoài đoạn AB về phía điện tích có độ lớn nhỏ hơn.còn nếu hai điện tích cùng dấu thì nằm giữa đoạn nối hai điện tích.
2. Ba điện tích:
- Điều kiện cân bằng của q0 khi chịu tác dụng bởi q1,q2,q3:
+ Gọi →F0 là tổng hợp lực do q1,q2,q3 tác dụng lên q0:
→F0=→F10+→F20+→F30=→0
+ Do q0 cân bằng: →F0=→0
⇒→F10+→F20+→F30=→0→F=→F10+→F20}⇒→F+→F30=→0⇔{→F↑↓→F30F=F30
Bài tập tự luyện có đáp án
Câu 1: Có 3 điện tích q1;q2;q3 đặt tại 3 điểm A,B,C trong không khí. Để q1 nằm cân bằng thì vị trí của A, B, C phải thỏa mãn
- A
- B
- C
- D
Để q1 nằm cân bằng ta có:
→F1=→F21+→F31=→0 ⇒→F21↑↓→F31
Do đó 3 điểm A, B, C thẳng hàng.
Câu 2: Hai điện tích điểm trái dấu được đặt tại 2 điểm A và B trong không khí. Hỏi phải đặt điện tích q0 ở đâu để q0 nằm cân bằng?
- A
- B
- C
- D
Để q0 nằm cân bằng thì lực điện tổng hợp:
→F0=→F1+→F2=→0 ⇔→F1↑↓→F2
Vì 2 điện tích trái dấu nên phải đặt điện tích q0 nằm trên đường AB và nằm ngoài khoảng 2 điện tích.
Câu 3: Hai điện tích điểm cùng dấu được đặt tại 2 điểm A và B trong không khí. Hỏi phải đặt điện tích q0 ở đâu để q0 nằm cân bằng?
- A
- B
- C
- D
Để q0 nằm cân bằng thì lực điện tổng hợp:
→F0=→F1+→F2=→0 ⇔→F1↑↓→F2
Vì 2 điện tích cùng dấu nên phải đặt điện tích q0 nằm trong đoạn AB, hay nằm trong khoảng 2 điện tích.
Câu 4: Có 4 điện tích điểm q1,q2,q3,q4 đặt tại 4 điểm trong không khí. Điều kiện để q4 nằm cân bằng là
- A
- B
- C
- D
Để q4 nằm cân bằng thì hợp lực tác dụng lên q4 :
→F4=→F14+→F24+→F34=→0
Xem thêm các bài tiếp theo bên dưới