Thời gian trong dao động điều hòa
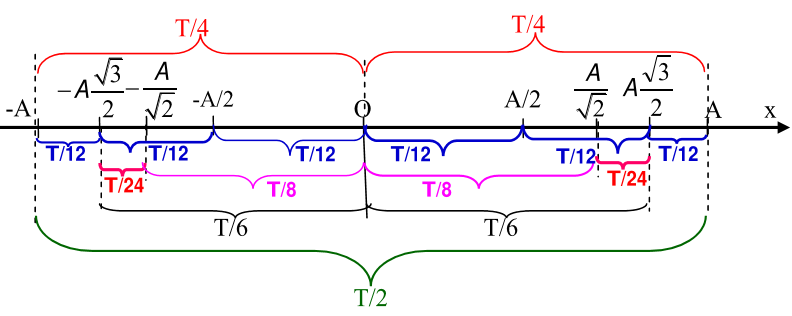
Lý thuyết về Thời gian trong dao động điều hòa
1. Khoảng thời gian ngắn nhất để vật đi từ vị trí có li độ x1 đến x2
$\Delta t=\dfrac{\Delta \varphi }{\omega }=\dfrac{\left| {{\varphi }_{2}}-{{\varphi }_{1}} \right|}{\omega }$ với $\left\{ \begin{align}& co\operatorname{s}{{\varphi }_{1}}=\dfrac{{{x}_{1}}}{A} \\ & co\operatorname{s}{{\varphi }_{2}}=\dfrac{{{x}_{2}}}{A} \\ \end{align} \right.$ và ($0\le {{\varphi }_{1}},{{\varphi }_{2}}\le \pi $)
VD: Vật dao động điều hòa với phương trình x = Acos(ωt + φ) (cm). Tính thời gian ngắn nhất vật đi từ vị trí có li độ ${{x}_{1}}=\dfrac{A\sqrt{3}}{2}$ đến vị trí có li độ x2 = -A/2.
HD: $\left. \begin{align}& \cos {{\varphi }_{1}}=\dfrac{{{x}_{1}}}{A}=\dfrac{\sqrt{3}}{2}\Rightarrow {{\varphi }_{1}}=\dfrac{\pi }{6} \\ & \cos {{\varphi }_{2}}=\dfrac{{{x}_{2}}}{A}=\dfrac{-1}{2}\Rightarrow {{\varphi }_{2}}=\dfrac{2\pi }{3} \\ \end{align} \right\}\Rightarrow \Delta \varphi =\left| {{\varphi }_{2}}-{{\varphi }_{1}} \right|=\dfrac{\pi }{2}\Rightarrow \Delta t=\dfrac{\Delta \varphi }{\omega }=\dfrac{\dfrac{\pi }{2}}{\dfrac{2\pi }{T}}=\dfrac{T}{4}$
2. Thời gian ngắn nhất
$\overline{{{v}_{tb}}}=\dfrac{S}{\Delta t}$
Trong đó $\overline{{{v}_{tb}}}$: là tốc độ trung bình của vật trong khoảng thời gian $\Delta t$
S là quãng đường vật đi được trong thời gian $\Delta t$
$\Delta t$ là thời gian vật dao động
Vật muốn đi hết quãng đường S trong khoảng thời gian ngắn nhất thì vật phải đi với tốc độ lớn nhất. Mà tốc độ của vật lớn nhà khi vật đi qua VTCB nên vật muốn đi hết quãng đường S trong thời gian ngắn nhất thì vật phải đi quanh VTCB.
Bài tập tự luyện có đáp án
Câu 1: Một chất điểm dao động điều hòa với chu kì T. Khoảng thời gian trong một chu kì để vật có tốc độ nhỏ hơn $ \dfrac{1}{3} $ tốc độ cực đại là:
- A
- B
- C
- D
Xét trong $ \dfrac{T}{4} $ vật có tốc độ nhỏ hơn $ \dfrac{1}{3} $ tốc độ cực đại khi đó góc quét được là góc $ \varphi $ như hình vẽ

Dựa vào đường tròn lượng giác: $ \text{sin}\varphi \text{=}\dfrac{{{v}_{\text{max}}}}{3{{v}_{\text{max}}}}=\dfrac{1}{3} $ $ \Rightarrow \varphi =0,11\pi $
Mà $ \varphi =\omega .\Delta t $ $ \Rightarrow \Delta t=\dfrac{\varphi }{\omega }=0,11\pi .\dfrac{T}{2\pi }=0,055T $
Xét trong một chu kì thời gian vật có tốc độ nhỏ hơn $ \dfrac{1}{3} $ tốc độ cực đại: 4.0,055T=0,22T