Quang phổ vạch của nguyên tử Hidro
Lý thuyết về Quang phổ vạch của nguyên tử Hidro
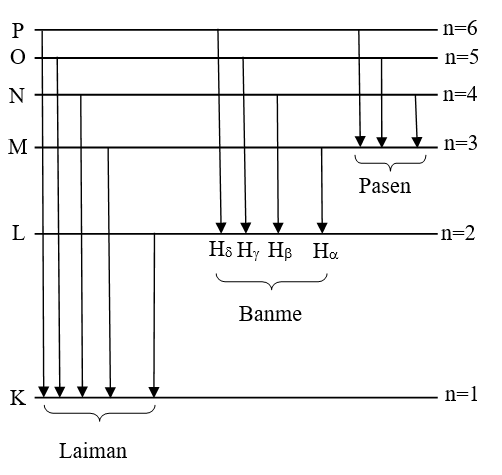
Sơ đồ mức năng lượng
- Dãy Laiman: Nằm trong vùng tử ngoại. Ứng với e chuyển từ quỹ đạo bên ngoài về quỹ đạo K
Lưu ý: Vạch dài nhất λ21 khi e chuyển từ L→K
Vạch ngắn nhất λ∞1 khi e chuyển từ ∞→K.
- Dãy Banme: Một phần nằm trong vùng tử ngoại, một phần nằm trong vùng ánh sáng nhìn thấy. Ứng với e chuyển từ quỹ đạo bên ngoài về quỹ đạo L
Vùng ánh sáng nhìn thấy có 4 vạch:
Vạch đỏ Hα ứng với e: M→L
Vạch lam Hβ ứng với e: N→L
Vạch chàm Hγ ứng với e: O→L
Vạch tím Hδ ứng với e: P→L
Lưu ý: Vạch dài nhất λ32 (Vạch đỏ Hα)
Vạch ngắn nhất λ∞L khi e chuyển từ ∞→L.
- Dãy Pasen: Nằm trong vùng hồng ngoại. Ứng với e chuyển từ quỹ đạo bên ngoài về quỹ đạo M
Lưu ý: Vạch dài nhất λ43 khi e chuyển từ N→M.
Vạch ngắn nhất λ∞M khi e chuyển từ ∞→M.
Mối liên hệ giữa các bước sóng và tần số của các vạch quang phổ của nguyên từ hiđrô:
1λ13=1λ12+1λ23 và f13=f12+f23 (như cộng véctơ)
Chú ý: Khi nguyên tử Hidro đang ở trạng thái ứng với mức năng lượng n, thì nguyên tử có thể phát xạ ra số bức xạ: N=C2n=n(n−1)2
Bài tập tự luyện có đáp án
Câu 1: Khi nói về phôtôn, phát biểu nào dưới đây đúng?
- A
- B
- C
- D
Theo thuyết lượng tử mỗi phôtôn có năng lượng xác định ε=hf=hcλ (1).
Dễ nhận thấy bước sóng càng lớn thì năng lượng càng bé. Tương tự, ánh sáng đỏ có bước sóng lớn hơn ánh sáng tím nên năng lượng ánh sáng tím lớn hơn năng lượng ánh sáng đỏ.
Một chú ý về phôtôn, nó chỉ tồn tại trong trạng thái chuyển động, không có phôtôn đứng yên.
Từ (1) ta có : với ánh sáng đơn sắc có f xác định, các phôtôn đều mang năng lượng như nhau và cùng bằng ε=hf .
Câu 2: Các nguyên tử hiđrô đang ở trạng thái dừng ứng với êlectron chuyển động trên quỹ đạo có bán kính lớn gấp 9 lần so với bán kính Bo. Khi chuyển về các trạng thái dừng có năng lượng thấp hơn thì các nguyên tử sẽ phát ra các bức xạ có tần số khác nhau. Có thể có nhiều nhất bao nhiêu tần số?
- A
- B
- C
- D
+ Bán kính quỹ đạo dứng là: r=n2r0=9r0⇒n=3
+ Khi chuyển về các trạng thái dừng có năng lượng thấp hơn thì các nguyên tử sẽ phát ra các bức xạ có tần số khác nhau. Có thể có nhiều nhất : 0,5.3(3 – 1) = 3
Câu 3: Hãy xác định trạng thái kích thích cao nhất của các nguyên tử hiđrô trong trường hợp người ta chỉ thu được 6 vạch quang phổ phát xạ của nguyên tử hiđrô
- A
- B
- C
- D
Khi electrôn chuyển từ quỹ đạo n vào quỹ đạo bên trong thì số bức xạ thứ cấp là:
0,5.n(n - 1) = 6 ⇔ n = 4
Trạng thái kích thích cao nhất ứng với quỹ đạo có n = 4 là quỹ đạo N
Câu 4: Gọi En là mức năng lượng của nguyên từ hidro ở trạng thái năng lượng ứng với quỹ đạo n (n > 1). Khi electron chuyển về các quỹ đạo bên trong thì có thể phát ra số bức xạ là:
- A
- B
- C
- D
Gọi En là mức năng lượng của nguyên từ hidro ở trạng thái năng lượng ứng với quỹ đạo n (n > 1). Khi electron chuyển về các quỹ đạo bên trong thì có thể phát ra số bức xạ là: 0,5.n(n - 1)
Câu 5: Chùm nguyên tử Hiđrô đang ở trạng thái cơ bản, bị kích thích phát sáng thì chúng có thể phát ra tối đa 3 vạch quang phổ. Khi bị kích thích electron trong nguyên tử H đã chuyển sang quỹ đạo?
- A
- B
- C
- D
Khi electrôn chuyển từ quỹ đạo n vào quỹ đạo bên trong thì số bức xạ thứ cấp là:
0,5.n(n - 1) = 3 ⇔ n = 3
Trạng thái kích thích cao nhất ứng với quỹ đạo có n = 3 là quỹ đạo M
Câu 6: Một nguyên tử hiđrô đang ở trạng thái cơ bản, hấp thụ một phôtôn có năng lượng ε0 và chuyển lên trạng thái dừng ứng với quỹ đạo N của êlectron. Từ trạng thái này, nguyên tử chuyển về các trạng thái dừng có mức năng lượng thấp hơn thì có thể phát ra phôtôn có năng lượng lớn nhất là
- A
- B
- C
- D
Nguyên tử phát ra photon có năng lượng lớn nhất ứng với chuyển về trạng thái cơ bản
⇒ photon có năng lượng ε0.
Câu 7: Khi nói về thuyết lượng tử ánh sáng, phát biểu nào sau đây là đúng?
- A
- B
- C
- D
Cường độ của chùm sáng tỉ lệ với số phôtôn phát ra trong 1 giây không phụ thuộc vào năng lượng của hạt phôtôn.
Phôtôn chỉ tồn tại trong trạng thái chuyển động, không có phôtôn đứng yên.
Mỗi phôtôn có năng lượng xác định ε=hf (f là tần số của sóng ánh sáng đơn sắc tương ứng), nên tần số càng lớn thì năng lượng càng lớn.
Thuyết lượng tử ánh sáng cho biết chùm ánh sáng là một chùm các phôtôn (các lượng tử ánh sáng)… có năng lượng xác định ε=hf .
Câu 8: Nguyên tử Hiđrô bị kích thích do chiếu xạ và electrôn của nguyên tử đã chuyển từ quỹ đạo K lên N. Sau khi ngừng chiếu xạ, nguyên tử Hiđrô phát xạ thứ cấp, phổ xạ này gồm
- A
- B
- C
- D
Khi electrôn chuyển từ quỹ đạo n vào quỹ đạo bên trong thì số bức xạ thứ cấp là: 0,5.n(n - 1)
Khi electrôn chuyển từ quỹ đạo N (có n = 4) vào quỹ đạo bên trong thì số bức xạ thứ cấp là:
0,5.4(4 - 1) = 6
Xem thêm các bài tiếp theo bên dưới