Mạch điện xoay chiều chứa R,C
Lưu về Facebook:
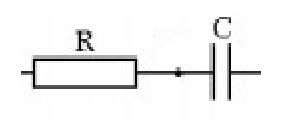
Lý thuyết về Mạch điện xoay chiều chứa R,C
→U=→UR+→UC
HĐT cực đại 2 đầu đoạn mạch: U0=√U20R+U20C
HĐT hiệu dụng 2 đầu đoạn mạch: U=√U2R+U2C
Tổng trở: Z=√R2+Z2C
u trễ pha hơn i 1 góc: tanφ=ZCR=UCUR=U0CU0R
Trong đó:
UR;UC là HĐT hiệu dụng 2 đầu điện trở và tụ điện.
U0R;U0C là HĐT cực đại 2 đầu điện trở và tụ điện.
ZC;R là dung kháng của tụ điện và điện trở.
Bài tập tự luyện có đáp án
Câu 1: Cho đoạn mạch gồm điện trở thuần R nối tiếp với tụ điện có điện dung C. Khi dòng điện xoay chiều có tần số góc ω chạy qua thì tổng trở của đoạn mạch là
- A
- B
- C
- D
Công thức tổng trở là:
√R2+(1ωC)2.
Câu 2: Trong một đoạn mạch điện xoay chiều không phân nhánh, cường độ dòng điện sớm pha φ so với điện áp ở hai đầu đoạn mạch (với 0<φ<0,5π). Đoạn mạch đó
- A
- B
- C
- D
Do 0<φ<0,5π nên mạch phải chứa điện trở R
i sớm pha hơn u nên mạch có chứa C
Xem thêm các bài tiếp theo bên dưới