Tính chất đường trung trực của một đoạn thẳng
Lý thuyết về Tính chất đường trung trực của một đoạn thẳng
Tính chất đường trung trực của một đoạn thẳng
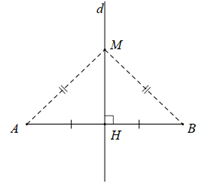
Định nghĩa: Đường trung trực của một đoạn thẳng là đường thẳng vuông góc với đoạn thẳng ấy tại trung điểm của nó.
Trên hình vẽ trên, $d$ là trung trực của đoạn thẳng $AB$. Ta cũng nói: $A$ đối xứng với $B$ qua $d$.
Định lí 1: Điểm nằm trên đường trung trực của một đoạn thẳng thì cách đều hai mút của đoạn thẳng đó.
Định lí 2: Điểm cách đều hai mút của đoạn thẳng thì nằm trên đường trung trực của đoạn thẳng đó.
$MA=MB\Rightarrow M$ thuộc đường trung trực của $AB$.
Nhận xét: Tập hợp các điểm cách đều hai mút của một đoạn thẳng là đường trung trực của đoạn thẳng đó.
Bài tập tự luyện có đáp án
Câu 1: Cho hai điểm M và N nằm trên đường trung trực của đoạn thẳng AB (M, N nằm khác phía đối với AB). Chọn khẳng định sai.
Chọn khẳng định sai.
- A
- B
- C
- D

M thuộc đường trung trực của đoạn thẳng AB nên $ MA=MB. $
N thuộc đường trung trực của đoạn thẳng AB nên $ NA=NB. $
$ \Rightarrow \Delta AMN=\Delta BMN\left( c.c.c \right)\Rightarrow \widehat{MAN}=\widehat{MBN};\,\,\widehat{MNB}=\widehat{MNA}. $
Vậy khằng định sai cần chọn là: " $ \,\widehat{MNB}=\widehat{MAN} $ ".
Câu 2: Cho tam giác ABC, đường phân giác AD. Trên tia AC lấy điểm E sao cho $ AE=AB. $ Chọn khẳng định sai.
Chọn khẳng định sai.
- A
- B
- C
- D

$ \Delta ABD=\Delta AED\left( c.g.c \right)\Rightarrow DB=DE $ ; $ \widehat{ADB}=\widehat{ADE} $ ; $ \widehat{ABD}=\widehat{AED} $
Ta có: $ DB=DE $ $ \Rightarrow $ Điểm D nằm trên đường trung trực của BE. (1)
Theo giả thiết: $ AB=AE $ $ \Rightarrow $ Điểm A nằm trên đường trung trực của BE. (2)
Từ (1) và (2) suy ra AD là đường trung trực của BE.
Vậy khẳng định sai cần chọn là: " $ \widehat{B}=\widehat{ADE} $ ".
Câu 3: Tam giác ABC có $ \widehat{B}-\widehat{C}={{40}^{0}}. $ Đường trung trực của BC cắt AC ở I. Số đo góc ABI là:
- A
- B
- C
- D

I thuộc trung trực của BC $ \Rightarrow IB=IC\Rightarrow \widehat{C}={{\widehat{B}}_{1}}. $
Ta lại có: $ \widehat{ABI}=\widehat{ABC}-{{\widehat{B}}_{1}}=\widehat{ABC}-\widehat{C}={{40}^{0}}. $
Câu 4: Cho điểm M thuộc đường trung trực của AB. Trên các đoạn thẳng MA, MB lấy theo thứ tự các điểm C, D sao cho $ AC=BD. $ Chọn khẳng định sai.
Chọn khẳng định sai.
- A
- B
- C
- D

M thuộc đường trung trực của AB nên $ MA=MB. $
Theo giả thiết: $ AC=BD $ nên $ MA-AC=MB-BD $ hay $ MC=MD. $
Suy ra M thuộc đường trung trực của CD.
Vậy khẳng định sai cần chọn là: "M không thuộc đường trung trực của AD".
Câu 5: Tam giác ABC có $ AB=6\,cm,\,\,BC=4cm. $ Qua trung điểm M của AC, kẻ đường vuông góc với AC, cắt AB ở I. Chu vi tam giác IBC là:
- A
- B
- C
- D

Ta có: IM là đường trung trực của AC $ \Rightarrow IA=IC. $
Chu vi $ \Delta IBC $ bằng: $ BC+BI+IC=BC+BI+IA $ $ =BC+BA=4+6=10\,(cm) $ .
Câu 6: Cho đoạn thẳng $ MN $ . Tập hợp điểm $ P $ sao cho $ \Delta PMN $ cân tại $ P $ là
- A
- B
- C
- D
Để $ \Delta PMN $ cân tại P thì PM = PN
Vậy điểm $ P $ luôn cách đều hai đầu mút đoạn thẳng MN nên P thuộc trung trực của đoạn thẳng $ MN $ .
Câu 7: Gọi M là một điểm nằm trên đường trung trực của đoạn thẳng AB. Cho biết $ \,AB=12cm, $ khoảng cách từ M đến đoạn thẳng AB bằng 8cm. Khi đó chu vi tam giác AMB là:
- A
- B
- C
- D

Kẻ MH vuông góc với AB (H thuộc AB) $ \Rightarrow \,\,MH=8cm $
Ta có: MH là đường trung trực của AB
$ \Rightarrow $ H là trung điểm của AB
$ \Rightarrow \,\,HA=HB=\dfrac{1}{2}AB=6cm. $
Xét tam giác AMH vuông tại H, theo định lí Py-ta-go ta có:
$ AM=\sqrt{M{{H}^{2}}+A{{H}^{2}}}=\sqrt{{{8}^{2}}+{{6}^{2}}}=10\,(cm) $ .
Vì M là một điểm nằm trên đường trung trực của đoạn thẳng AB nên $ MA=MB=10cm. $
Chu vi tam giác MAB là: $ MA+MB+AB=10+10+12=32\,(cm). $
Câu 8: Cho $ \Delta ABC\,\,\left( \widehat{A} > {{90}^{0}} \right) $ có đường trung trực của $ BC $ cắt cạnh $ AC $ tại điểm $ D $ , biết $ BD=11cm,\text{ }\,AC=5cm $ . Độ dài cạnh $ AD $ bằng
- A
- B
- C
- D
Do $ D $ thuộc đường trung trực của $ BC\Rightarrow DC=BD=11cm $
Mà $ DC=DA+AC\Rightarrow DA=DC-AC=11-5=6 $ cm.
Câu 9: Tam giác ABC có $ AB < AC. $ Gọi d là đường trung trực của BC, E là giao điểm của d với AC. Gọi K là một điểm bất kì thuộc d (K khác E). Chọn khẳng định đúng.
Chọn khẳng định đúng.
- A
- B
- C
- D

Theo tính chất đường trung trực: $ EB=EC,KB=KC. $
Ta có: $ AK+KB=AK+KC > AC=AE+EC=AE+EB. $
$ \Rightarrow AB+AK+KB > AB+AE+EB. $
Vậy chu vi $ \Delta AKB $ lớn hơn chu vi $ \Delta AEB. $
Câu 10: Cho tam giác ABC cân tại A. Trên các cạnh AB và AC lần lượt lấy các điểm M và N sao cho $ AM+AN=AB. $ Đường trung trực của AB cắt tia phân giác của góc A tại O. Khẳng định nào sau đây là đúng ?
- A
- B
- C
- D

Ta có: $ AM+MB=AB $ (M thuộc AB).
Mà $ AM+AN=AB $ (theo giả thiết)
$ \Rightarrow \,\,MB=AN $ .
Xét $ \Delta AON $ và $ \Delta BOM $ có:
$ OA=OB $ (Vì O nằm trên đường trung trực của AB);
$ AN=MB $ (theo chứng minh trên);
$ \widehat{MBO}={{\widehat{A}}_{2}} $ (Vì cùng bằng $ {{\widehat{A}}_{1}} $ )
$ \Rightarrow \,\Delta AON=\Delta BOM\,(c.g.c) $
$ \Rightarrow \,OM=ON $
$ \Rightarrow $ O nằm trên đường trung trực của MN.
Vậy khẳng định đúng cần chọn là: "O nằm trên đường trung trực của MN".
Câu 11: Cho tam giác ABC vuông tại A, có $ AB > AC. $ Đường trung trực của cạnh huyền BC cắt AB tại D. Lấy M là một điểm tùy ý trên đoạn BD. Gọi H là hình chiếu của A trên đường thẳng BC. Chọn khẳng định đúng.
Chọn khẳng định đúng.
- A
- B
- C
- D

Gọi E là giao của đường trung trực của BC với BC.
$ \Rightarrow $ E là trung điểm của BC.
Vì các góc B và C nhọn nên H nằm trên cạnh BC.
Ta có: độ dài đường xiên AB lớn hơn độ dài đường xiên AC.
$ \Rightarrow $ Độ dài hình chiếu HB lớn hơn độ dài hình chiếu HC.
Vì điểm D nằm trên đường trung trực của BC nên $ DB=DC $ .
Tam giác ACD vuông tại A nên $ AD < CD\,\,\Rightarrow \,\,AD < BD $ .
Vậy khẳng định đúng cần chọn là: " $ DC=DB $ ".
Câu 12: Chọn khẳng định sai. Cho đoạn thẳng $ AB $ , $ M $ là trung điểm của $ AB $ . $ I $ là điểm bất kì sao cho $ IA=IB $ .
Cho đoạn thẳng $ AB $ , $ M $ là trung điểm của $ AB $ . $ I $ là điểm bất kì sao cho $ IA=IB $ .
- A
- B
- C
- D
Ta có $ \Delta IAB $ có $ IA=IB $ nên tam giác $ \Delta IAB $ cân tại I.
Lại có $ M $ là trung điểm của $ AB $ nên IM là đường trung tuyến hạ từ đỉnh I
Nên IM vừa là đường trung tuyến vừa là đường phân giác và là đường trung trực của $ \Delta IAB $
$ \Rightarrow MI\bot AB $ .
Câu 13: Cho ba tam giác cân ABC, DBC, EBC có chung đáy BC. Chọn khẳng định sai.
Chọn khẳng định sai.
- A
- B
- C
- D

$ AB=AC\Rightarrow $ A thuộc đường trung trực của đoạn thẳng BC.
$ DB=DC\Rightarrow $ D thuộc đường trung trực của đoạn thẳng BC.
$ EB=EC\Rightarrow $ E thuộc đường trung trực của đoạn thẳng BC.
Khi đó ba điểm A, D, E thẳng hàng.
Vậy khẳng định sai cần chọn là: "E thuộc đường trung trực của đoạn thẳng AB".