Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt
Lý thuyết về Hình nón. Hình nón cụt. Diện tích xung quanh và thể tích của hình nón, hình nón cụt
1. Khái niệm hình nón
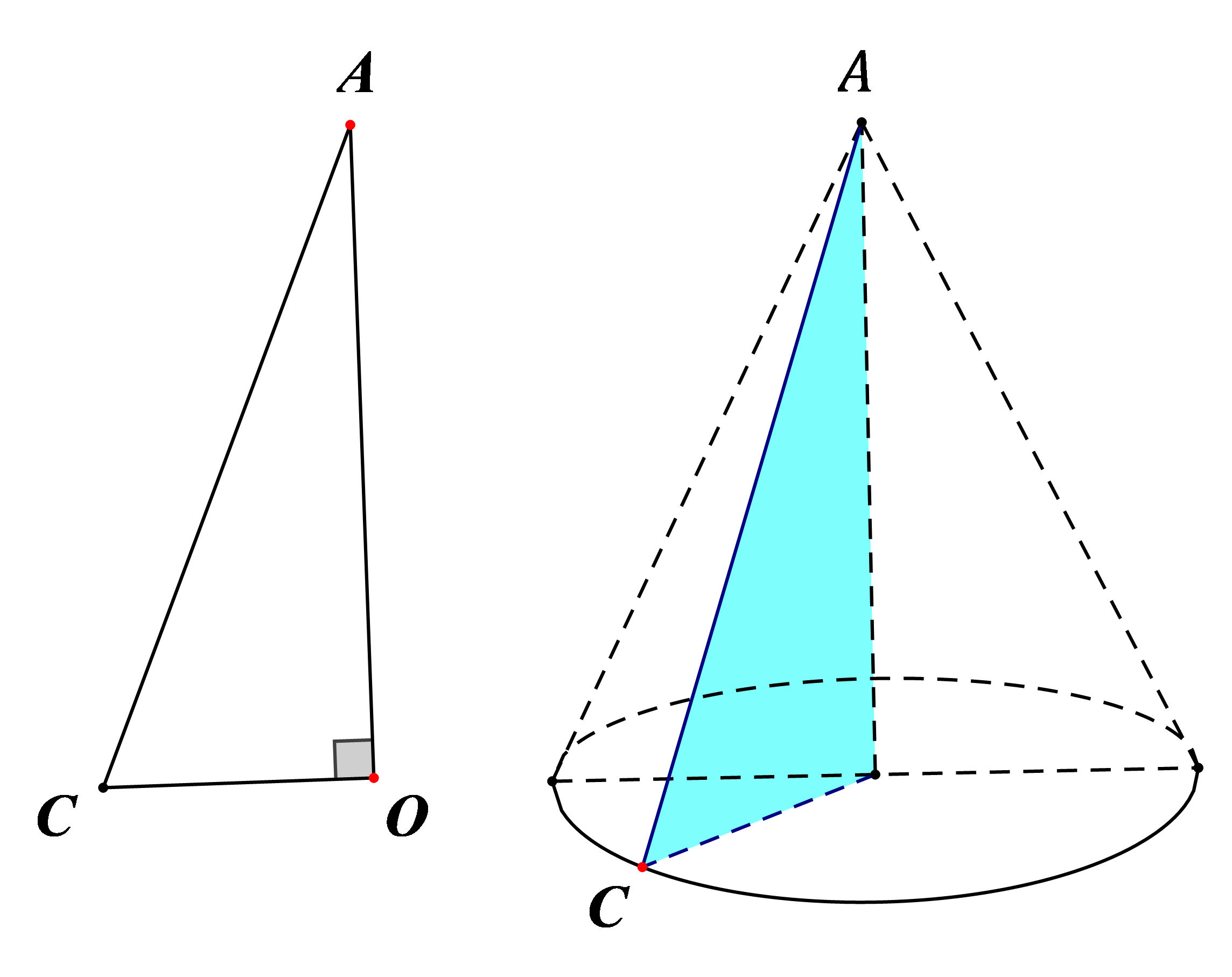
Khi quay một tam giác vuông góc AOC một vòng quanh cạnh góc vuông OA cố định thì được một hình nón.
– Cạnh OC tạo nên đáy của hình nón, là một hình nón tâm O.
– Cạnh AC quét lên mặt xung quanh của hình nón, mỗi vị trí của nó được gọi là một đường sinh, chẳng hạn AD là một đường sinh .
– A là đỉnh và AO là đường cao của hình nón
2. Diện tích xung quanh, diện tích toàn phần của hình nón
Diện tích xung quanh của hình nón: Sxq=2πrl
Diện tích toàn phần của hình nón: Stp=πrl+πr2
(r là bán kính đường tròn đáy, l là đường sinh)
3. Thể tích hình nón
Công thức tính thể tích hình nón: V=13πr2h
Diện tích toàn phần của hình nón: Stp=πrl+πr2
(r là bán kính đường tròn đáy, l là đường sinh)
4. Thể tích hình nón cụt
Vnc=13π(r21+r22+r1r2)h
Sxq=π(r1+r2)l
Stp=π(r1+r2)l+πr21+πr22
Bài tập tự luyện có đáp án
Câu 1: Cho hình nón có chiều cao h=10cm và thể tích V=1000π(cm3) . Tính diện tích toàn phần của hình nón.
- A
- B
- C
- D
Ta có V=13πR2h⇔13πR2.10=1000π⇒R2=300⇒R=10√3 Và R2+h2=l2⇔102+(10√3)2=l2⇔l=20cm
Diện tích toàn phần của hình nón là Stp=πRl+πR2=π.10√3.20+π.300=(300+200√3)π(cm2) .
Câu 2: Một chiếc xô hình nón cụt làm bằng tôn để đựng nước.Các bán kính đáy là 12cm và 6cm chiều cao là 15cm . Tính dung tích của xô là
- A
- B
- C
- D
Ta có V=13πh(R2+Rr+r2)=13π.15.(122+12.6+62)=1260π(cm3) .
Câu 3: Một chiếc xô hình nón cụt làm bằng tôn để đựng nước. Các bán kính đáy là 10cm và 5cm chiều cao là 20cm . Tính dung tích của xô là
- A
- B
- C
- D
Ta có V=13πh(R2+Rr+r2)=13π.20.(102+10.5+52)=3500π3(cm3)
Câu 4: Hình nón cụt có bán kính đáy lớn R , bán kính đáy nhỏ r và chiều cao h có thể tích là:
- A
- B
- C
- D
Hình nón cụt có bán kính đáy lớn R , bán kính đáy nhỏ r và chiều cao h có thể tích là V=13π(R2+Rr+r2)h
Câu 5: Một hình nón có bán kính là 4cm, chiều cao bằng 3cm. Thể tích của hình nón bằng:
- A
- B
- C
- D
Thể tích của hình nón bằng: V=13.π.r2.h=13.π.42.3=16π(cm3).
Câu 6: Cho hình nón có bán kính đáy R=3(cm) và chiều cao h=4(cm) . Diện tích xung quanh của hình nón là
- A
- B
- C
- D
Vì R2+h2=l2⇔32+42=l2⇔l2=25⇒l=5cm
Diện tích xung quanh của hình nón là Sxq=πRl=π.3.5=15π(cm2) .