Công thức tính độ dài đường tròn, cung tròn
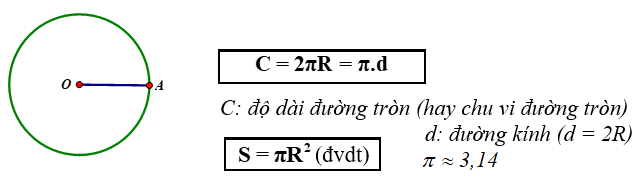
Lý thuyết về Công thức tính độ dài đường tròn, cung tròn
1. Độ dài đường tròn (O;R)
2. Cách tính độ dài cung tròn
Bài tập tự luyện có đáp án
Câu 1: Cho C = 3,14. Hãy điền vào các bảng sau: 
Áp dụng công thức $ C=2\pi R=\pi d;S=\pi {{R}^{2}}=\pi \dfrac{{{d}^{2}}}{4} $ ta có bảng sau:
Câu 2: Tính chu vi vành xe đạp có đường kính 600mm.
Bán kính vành xe là 300 (mm).
Chu vi vành xe là $ 2\pi .300=600\pi $ (mm).
Câu 3: Cho hai đường tròn cùng bán kính $ \left( O;R \right) $ và $ \left( O';R \right) $ . Gọi $ A,B $ là hai điểm thuộc $ \left( O;R \right) $ và $ C,D $ là hai điểm thuộc $ \left( O';R \right) $ sao cho độ dài cung nhỏ $ AB $ gấp đôi độ dài cung nhỏ $ CD $ .
- A
- B
- C
- D
Đặt $ \widehat{AOB}=\alpha ,\widehat{COD}=\beta $ . Khi đó:
+ Độ dài cung $ AB $ là $ \dfrac{\pi R\alpha }{{{180}^{0}}} $ .
+ Đồ dài cung $ CD $ là $ \dfrac{\pi R\beta }{{{180}^{0}}} $ .
Mà độ dài cung nhỏ $ AB $ gấp đôi độ dài cung nhỏ $ CD $ nên $ \dfrac{\pi R\alpha }{{{180}^{0}}}=2.\dfrac{\pi R\beta }{{{180}^{0}}}\Leftrightarrow \alpha =2\beta $ .
Vậy $ \widehat{AOB}=2\widehat{COD} $ .
Câu 4: Cho tam giác $ ABC $ có $ AB=AC=3\,\,cm,\,\,\widehat{\text{A}}={{120}^{o}}. $ Độ dài đường tròn ngoại tiếp tam giác $ ABC $ là:
- A
- B
- C
- D

Gọi $ O $ là tâm đường tròn ngoại tiếp tam giác $ ABC $ .
Vì tam giác $ ABC $ cân tại $ A $ nên $ AO $ vừa là đường cao vừa là phân giác của $ \widehat{BAC} $
Suy ra $ \widehat{CAO}=\dfrac{120{}^\circ }{2}=60{}^\circ $ .
Xét tam giác $ CAO $ có $ OA=OC;\widehat{CAO}=60{}^\circ \Rightarrow \Delta CAO $ đều nên $ OA=OC=AC=3\,cm $ .
Do đó bán kính đường tròn ngoại tiếp $ \Delta ABC $ là $ R=3\,cm $ .
Chu vi đường tròn $ \left( O \right) $ là $ C=2\pi R=6\pi \,\,\left( cm \right) $ .
Câu 5: Cho đường tròn (O, 5cm), đường kính AB. Điểm $ M\in (O) $ sao cho $ \widehat{MAB}={{45}^{0}} $ . Độ dài cung MB là:
- A
- B
- C
- D

Xét đường tròn (O) có:
Góc MAB là góc nội tiếp chắn cung BM $ \Rightarrow \overset\frown{MB}=2\widehat{MAB}={{2.90}^{0}}={{180}^{0}}. $
Vậy độ dài cung MB là $ \ell =\dfrac{\pi Rn}{180}=\dfrac{\pi .5.90}{180}=\dfrac{5\pi }{2} $ (cm).
Câu 6: Một đường tròn có độ dài là 30 cm. Tìm độ dài đường kính của đường tròn.
Bán kính đường tròn là $ \dfrac{30}{2\pi }=\dfrac{15}{\pi } $ (cm).
Đường kính đường tròn là $ 2.\dfrac{15}{\pi }=\dfrac{30}{\pi } $ (cm).
Câu 7: Lấy giá trị gần đúng của n là 3,14, hãy điền vào ô trông trong bảng sau (đon vị độ dài: cm, làm tròn kết quả đến chữ số thập phân thứ nhất và đến độ): 
Áp dụng công thức tính độ dài cung có số đo $ n{}^\circ $ là $ 2\pi R.\dfrac{n{}^\circ }{360{}^\circ } $ ta có bảng sau:
Câu 8: Lấy giá trị gần đúng của a là 3,14, hãy điền vào ô trống trong bảng sau (đơn vị độ dài: cm, làm tròn kết quả đến chữ số thập phân thứ nhất và đến độ): 
Áp dụng công thức tính độ dài cung có số đo $ n{}^\circ $ là $ 2\pi R.\dfrac{n{}^\circ }{360{}^\circ } $ ta có bảng sau: