Dấu hiệu nhận biết tiếp tuyến của đường tròn
Lý thuyết về Dấu hiệu nhận biết tiếp tuyến của đường tròn
* Định nghĩa tiếp tuyến của đường tròn:
- Đường thẳng được gọi là tiếp tuyến của đường tròn nếu nó có một điểm chung với đường tròn. Điểm đó được gọi là tiếp điểm
Ví dụ: ΔΔ là tiếp tuyến của đường tròn (O)(O), HH gọi là tiếp điểm
*Tính chất:
-Tiếp tuyến của đường tròn vuông góc với bán kính tại tiếp điểm.
*Dấu hiệu nhận biết:
- Nếu một đường thẳng đi qua 1 điểm của đường tròn và vuông góc với bán kính đi qua điểm đó thì đường thẳng ấy là một tiếp tuyến của đường tròn
Bài tập tự luyện có đáp án
Câu 1: Cho đường tròn (O;R)(O;R) đường kính ABAB . Vẽ dây ACAC sao cho ^ABC=30∘ˆABC=30∘ . Trên tia đối của tia ABAB lấy điểm MM sao cho AM=RAM=R . Tính độ dài MCMC theo RR .
- A
- B
- C
- D
Áp dụng định lý Pytago cho tam giác vuông OCMOCM , ta có OM2=OC2+MC2OM2=OC2+MC2
⇒MC2=OM2−OC2=3R2⇒MC=√3R⇒MC2=OM2−OC2=3R2⇒MC=√3R .
Câu 2: Hình chữ nhật ABCDABCD , HH là hình chiếu của AA lên BDBD . M,NM,N lần lượt là trung điểm của BH,CDBH,CD . Đường nào sau đây là tiếp tuyến của đường tròn tâm AA , bán kính AMAM .
- A
- B
- C
- D
Lấy EE là trung điểm của AHAH . Do MM là trung điểm của BHBH (gt) nên EMEM là đường trung bình của ΔAHBΔAHB .
⇒EM//AB⇒EM//AB và EM=12ABEM=12AB .
Hình chữ nhật ABCDABCD có CD//ABCD//AB và CD=ABCD=AB mà NN là trung điểm của DCDC , suy ra
DN//ABDN//AB và DN=12ABDN=12AB .
Từ (1) và (2) ta có EM//DNEM//DN và EM=DNEM=DN .
Suy ra tứ giác EMNDEMND là hình bình hành, do đó DI//MNDI//MN .
Do EM//ABEM//AB mà AB⊥ADAB⊥AD (tính chất hình chữ nhật)
AH⊥DMAH⊥DM (gt) nên EE là trực tâm của ΔADMΔADM
Suy ra DE⊥AMDE⊥AM , mà DE//MNDE//MN (cmt)
⇒MN⊥AM⇒MN⊥AM tại MM .
Vì vậy MNMN là tiếp tuyến của đường tròn (A;AM)(A;AM) .
Câu 3: Cho tam giác ABCABC có hai đường cao BD,CEBD,CE cắt nhau tại HH . Xác định tâm FF của đường tròn đi qua bốn điểm A,D,H,EA,D,H,E .
- A
- B
- C
- D
Gọi FF là trung điểm của AHAH
Xét hai tam giác vuông AEHAEH và ADHADH ta có FA=FH=FE=FD=AH2FA=FH=FE=FD=AH2
Nên bốn đỉnh A,D,H,EA,D,H,E cùng thuộc đường tròn tâm FF bán kính AH2AH2 .
Câu 4: Từ một điểm AA ở bên ngoài đường tròn (O;R)(O;R) , vẽ hai tiếp tuyến AB,ACAB,AC với (O)(O) . Đường thẳng vuông góc với OBOB tại OO cắt tia ACAC tại NN . Đường thẳng vuông góc với OCOC cắt tia ABAB tại MM . Tứ giác AMONAMON là hình gì?
- A
- B
- C
- D
Dễ có AMONAMON là hình bình hành (Vì ON//AM;OM//ANON//AM;OM//AN )
Ta chứng minh OM=ONOM=ON
Xét tam giác OBMOBM và tam giác OCNOCN có:
^OBM=^OCN=90∘ˆOBM=ˆOCN=90∘ ;
OB=OC=ROB=OC=R ,
Và ^OMB=^ONC=ˆAˆOMB=ˆONC=ˆA
⇒ΔOBM=ΔOCN⇒ΔOBM=ΔOCN
⇒OM=ON⇒AMON⇒OM=ON⇒AMON là hình thoi.
Câu 5: Cho đường tròn (O;R)(O;R) đường kính ABAB . Vẽ dây ACAC sao cho ^ABC=30∘ˆABC=30∘ . Trên tia đối của tia ABAB lấy điểm MM sao cho AM=RAM=R . Chọn khẳng định đúng.
- A
- B
- C
- D
Tam giác OBCOBC cân tại OO có ^ABC=30∘ˆABC=30∘ suy ra ^AOC=60∘ˆAOC=60∘ (góc ngoài tại một đỉnh bằng tổng hai góc trong không kề với nó).
Nên tam giác OCAOCA là tam giác đều suy ra AC=AO=AM=R⇒^OCM=90∘⇒MCAC=AO=AM=R⇒ˆOCM=90∘⇒MC là tiếp tuyến của (O;R)(O;R) .
Câu 6: Cho tam giác ABCABC vuông tại AA , đường cao AHAH . Đường tròn đường kính BHBH cắt ABAB tại DD , đường tròn đường kính CHCH cắt ACAC tại EE . Chọn khẳng định sai.
- A
- B
- C
- D
Gọi I,JI,J lần lượt là trung điểm của BHBH và CHCH .
Để chứng minh DEDE là tiếp tuyến của đường tròn tâm II đường kính BHBH ta chứng minh ID⊥DEID⊥DE hay ^ODI=90∘ˆODI=90∘ .
Vì D,ED,E lần lượt thuộc đường tròn đường kính BHBH và HCHC nên ta có: ^BDH=^CEH=90∘ˆBDH=ˆCEH=90∘
Suy ra tứ giác ADHEADHE là hình chữ nhật.
Gọi OO là giao điểm của AHAH và DEDE , khi đó ta có OD=OH=OE=OAOD=OH=OE=OA .
Suy ra ΔODHΔODH cân tại O⇒^ODH=^OHDO⇒ˆODH=ˆOHD
Ta cũng có ΔIDHΔIDH cân tại I⇒^IDH=^IHDI⇒ˆIDH=ˆIHD
Từ đó ⇒^IDH+^HDO=^IHD+^DHO⇒^IDO=90∘⇒ID⊥DE⇒ˆIDH+ˆHDO=ˆIHD+ˆDHO⇒ˆIDO=90∘⇒ID⊥DE
Ta có ID⊥DE,D∈(I)ID⊥DE,D∈(I) nên DEDE là tiếp tuyến của đường tròn đường kính BHBH .
Câu 7: Cho hình vẽ dưới đây. Biết ABAB và ACAC là hai tiếp tuyến của (O),^BAC=120∘,AO=8cm(O),ˆBAC=120∘,AO=8cm . 
Độ dài đoạn ABAB là
Độ dài đoạn ABAB là
- A
- B
- C
- D
Từ hình vẽ ta có AB;ACAB;AC là tiếp tuyến của (O)(O) tại B,CB,C suy ra OB⊥ABOB⊥AB tại BB và OC⊥ACOC⊥AC tại CC .
Suy ra ΔABO=ΔACOΔABO=ΔACO (c – g – c) nên ^BAO=^CAO=^BAC2=60∘ˆBAO=ˆCAO=ˆBAC2=60∘
Xét ΔABOΔABO có AB=AO.cosA=8.cos60∘=4cmAB=AO.cosA=8.cos60∘=4cm .
Câu 8: Cho hình vẽ dưới đây: Biết ^BAC=60∘ˆBAC=60∘ ; AO=10cmAO=10cm . 
Độ dài tiếp tuyến ABAB là
Độ dài tiếp tuyến ABAB là
- A
- B
- C
- D
Ta có AB;ACAB;AC là tiếp tuyến của (O)(O) tại B,CB,C suy ra OC⊥ACOC⊥AC tại CC .
Suy ra ΔABO=ΔACOΔABO=ΔACO (c – g – c) nên ^BAO=^CAO=^BAC2=30∘ˆBAO=ˆCAO=ˆBAC2=30∘
Xét ΔABOΔABO có AB=AO.cosA=10.cos30∘=5√3cmAB=AO.cosA=10.cos30∘=5√3cm .
Câu 9: Cho nửa đường tròn đường kính ABAB . CC là một điểm thuộc nửa đường tròn. Vẽ dây BDBD là phân giác của góc ABCABC . BDBD cắt ACAC tại EE . ADAD cắt BCBC tại GG . HH là điểm đối xứng với EE qua DD . Chọn đáp án đúng nhất. Tứ giác AHGEAHGE là hình gì?
- A
- B
- C
- D
Vì DD thuộc đường tròn đường kính ABAB nên BD⊥AD⇒BDBD⊥AD⇒BD là đường cao của ΔABGΔABG , mà BDBD là đường phân giác của ABGABG (gt) nên BDBD vừa là đường cao vừa là đường phân giác của ΔABGΔABG .
Do đó ΔABGΔABG cân tại BB suy ra BDBD là trung trực của AGAG (1).
Vì HH đối xứng với EE qua DD (gt) nên DD là trung điểm của HEHE (2)
Từ (1) và (2) suy ra DD là trung điểm của HEHE và AGAG
Do đó tứ giác AHGEAHGE là hình bình hành (dấu hiệu nhận biết hình bình hành)
Mà HE⊥AGHE⊥AG nên ΔHGEΔHGE là hình thoi (dấu hiệu nhận biết hình thoi).
Câu 10: Cho đường tròn (O)(O) , dây ABAB khác đường kính. Qua OO kẻ đường vuông góc với ABAB , cắt tiếp tuyến tại AA của đường tròn ở điểm CC . Cho bán kính của đường tròn bằng 15cm;AB=24cm15cm;AB=24cm . Tính OCOC .
- A
- B
- C
- D
Gọi II là giao điểm của OCOC và AB⇒AI=BI=AB2=12cmAB⇒AI=BI=AB2=12cm .
Xét tam giác vuông OAIOAI có OI=√OA2−AI2=9cmOI=√OA2−AI2=9cm
Xét tam giác vuông AOCAOC có AO2=OI.OC⇒OC=AO2OI=1529=25cmAO2=OI.OC⇒OC=AO2OI=1529=25cm .
Vậy OC=25cmOC=25cm .
Câu 11: Cho hình vẽ dưới đây: Biết ^BAC=60∘ˆBAC=60∘ ; AO=10cmAO=10cm . 
Độ dài bán kính OBOB là
Độ dài bán kính OBOB là
- A
- B
- C
- D
Từ hình vẽ ta có AB;ACAB;AC là tiếp tuyến của (O)(O) tại B,CB,C suy ra OC⊥ACOC⊥AC tại CC .
Suy ra ΔABO=ΔACOΔABO=ΔACO (c – g – c) nên ^BAO=^CAO=^BAC2=30∘ˆBAO=ˆCAO=ˆBAC2=30∘
Xét ΔABOΔABO có OB=AO.sinA=10.sin30∘=5cmOB=AO.sinA=10.sin30∘=5cm .
Câu 12: Cho tam giác ABCABC cân tại AA ; đường cao AHAH và BKBK cắt nhau tại II . Khi đó đường thẳng nào sau đây là tiếp tuyến của đường tròn đường kính AIAI .
- A
- B
- C
- D
Gọi OO là trung điểm AIAI . Xét tam giác vuông AIKAIK có OK=OI=OA⇒K∈(O;AI2)OK=OI=OA⇒K∈(O;AI2) (*)
Ta đi chứng minh OK⊥KHOK⊥KH tại KK .
Xét tam giác OKAOKA cân tại OO ta có: ^OKA=^OKAˆOKA=ˆOKA (1)
Vì tam giác ABCABC cân tại AA có đường cao AHAH nên HH là trung điểm của BCBC . Xét tam giác vuông BKCBKC có HK=HB=HC=BC2HK=HB=HC=BC2 .
Suy ra tam giác KHBKHB cân tại HH nên ^HKB=^HBKˆHKB=ˆHBK (2)
Mà ^HBK=^KAHˆHBK=ˆKAH (cùng phụ với ^ACBˆACB ) (3)
Từ (1); (2); (3) suy ra ^HKB=^AKOˆHKB=ˆAKO mà ^AKO+^OKI=90∘⇒^HKB+^OKI=90∘⇒^OKH=90∘ˆAKO+ˆOKI=90∘⇒ˆHKB+ˆOKI=90∘⇒ˆOKH=90∘ hay OK⊥KHOK⊥KH tại KK (**)
Từ (*) và (**) thì HKHK là tiếp tuyến của đường tròn đường kính AIAI .
Câu 13: Cho đường tròn (O)(O) , dây MNMN khác đường kính. Qua OO kẻ đường vuông góc với MNMN , cắt tiếp tuyến tại MM của đường tròn ở điểm PP . Cho bán kính của đường tròn bằng 10cm;MN=12cm10cm;MN=12cm . Tính OPOP .
- A
- B
- C
- D
Gọi II là giao điểm của MNMN và OPOP
Ta có OP⊥MNOP⊥MN tại I⇒II⇒I là trung điểm của MNMN .
nên IM=MN2=122=6cmIM=MN2=122=6cm
xét tam giác vuông OMIOMI có OI=√OM2−MI2=√102−62=8cmOI=√OM2−MI2=√102−62=8cm
xét tam giác vuông MPOMPO theo hệ thức lượng trong tam giác vuông ta có:
MO2=OI.OP⇒OP=MO2OI=1028=12,5cmMO2=OI.OP⇒OP=MO2OI=1028=12,5cm
Vậy OP=12,5cmOP=12,5cm .
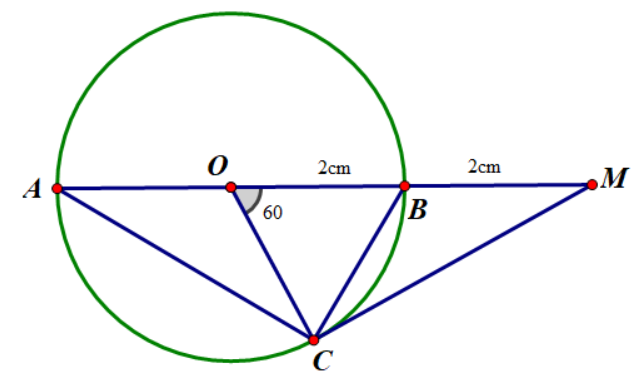
Câu 14: Cho đường tròn (O;2cm)(O;2cm) đường kính ABAB . Vẽ dây ACAC sao cho ^OBC=60∘ˆOBC=60∘ . Trên tia OBOB lấy điểm MM sao cho BM=2cmBM=2cm . Tính độ dài MCMC .
- A
- B
- C
- D

Theo ta có ΔOCMΔOCM vuông tại CC
Áp dụng định lý Pytago cho tam giác vuông OCMOCM , ta có OM2=OC2+MC2OM2=OC2+MC2
⇒MC2=OM2−OC2=42−22=12⇒MC=2√3cm⇒MC2=OM2−OC2=42−22=12⇒MC=2√3cm .
Câu 15: Cho đường tròn (O;2cm)(O;2cm) đường kính ABAB . Vẽ dây ACAC sao cho ^OBC=60∘ˆOBC=60∘ . Trên tia OBOB lấy điểm MM sao cho BM=2cmBM=2cm . Chọn khẳng định đúng.
- A
- B
- C
- D

Tam giác OBCOBC cân tại OO có ^OBC=60∘ˆOBC=60∘
Nên tam giác OCBOCB là tam giác đều suy ra BC=OB=OC=2BC=OB=OC=2
Xét tam giác OCMOCM có BC=OB=BM=2=OM2BC=OB=BM=2=OM2 nên ΔOCMΔOCM vuông tại CC
⇒OC⊥CM⇒MC⇒OC⊥CM⇒MC là tiếp tuyến của (O;2cm)(O;2cm) .
Câu 16: Cho đường tròn (O)(O) , dây ABAB khác đường kính. Qua OO kẻ đường vuông góc với ABAB , cắt tiếp tuyến tại AA của đường tròn ở điểm CC . Chọn khẳng định đúng?
- A
- B
- C
- D
Ta có OC⊥AB⇒OCOC⊥AB⇒OC đi qua trung điểm của ABAB .
⇒OC⇒OC là đường cao đồng thời là trung tuyến của ΔABCΔABC .
⇒ΔABC⇒ΔABC cân tại CC .
⇒{^ACO=^BCOAC=CB⇒ΔAOC=ΔBOC (c – g – c)
⇒OB⊥BC
⇒BC là tiếp tuyến của (O)
Câu 17: Cho tam giác ABC có hai đường cao BD,CE cắt nhau tại H . Gọi M là trung điểm BC . Đường tròn (F) ở trên nhận các đường thẳng nào dưới đây là tiếp tuyến.
- A
- B
- C
- D
AH cắt BC tại K⇒AK⊥BC vì H là trực tâm tam giác ABC
Ta chứng minh ME⊥EF tại E .
ΔFAE cân tại F (vì FA=FE ) nên ^FEA=^FAE
ΔMEC cân tại M (vì ME=MC=MB=BC2 ) nên ^MEC=^MCE mà ^BAK=^ECB (cùng phụ với ^ABC )
Nên ^MEC=^FEA⇒^MEC+^FEC=^FEA+^FEC⇒^MEF=90∘⇒ME⊥EF tại E .
Từ đó ME là tiếp tuyến của (F;AH2) .
Tương tự ta cũng có MF là tiếp tuyến của (F;AH2) .
Câu 18: Từ một điểm A ở bên ngoài đường tròn (O;R) , vẽ hai tiếp tuyến AB,AC với (O) . Đường thẳng vuông góc với OB tại O cắt tia AC tại N . Đường thẳng vuông góc với OC cắt tia AB tại M . Điểm A phải cách O một khoảng là bao nhiêu để cho MN là tiếp tuyến của (O) ?
- A
- B
- C
- D
Tứ giác AMON là hình thoi nên OA⊥MN và
Mà độ dài OA bằng 2 lần khoảng cách từ O đến MN .
Do đó MN là tiếp tuyến đường tròn (O;R)⇔ khoảng cách từ O đến MN bằng R⇔OA=2R .
Câu 19: Cho hình vẽ dưới đây. Biết AB và AC là hai tiếp tuyến của (O),^BAC=120∘,AO=8cm . 
Độ dài bán kính OB là
Độ dài bán kính OB là
- A
- B
- C
- D
Dễ dàng ta có AB;AC là tiếp tuyến của (O) tại B,C suy ra OC⊥AC tại C .
Suy ra ΔABO=ΔACO (c – g – c) nên ^BAO=^CAO=^BAC2=60∘
Xét ΔABO có OB=AO.sinA=10.sin60∘=4√3cm .
Câu 20: Cho đường tròn (O) , dây MN khác đường kính. Qua O kẻ đường vuông góc với MN , cắt tiếp tuyến tại M của đường tròn ở điểm P . Chọn khẳng định đúng?
- A
- B
- C
- D
Gọi I là giao điểm của MN và OP
Ta có OP⊥MN tại I⇒I là trung điểm của MN .
⇒PI là đường cao đồng thời là trung tuyến của ΔMNP
⇒ΔMNP cân tại P
⇒{^MPO=^NPOPM=PN⇒ΔPMO=ΔPNO (c – g – c)
⇒^PMO=^PNO=90∘⇒ON⊥NP
⇒PN là tiếp tuyến của (O)