Hình trụ và khối trụ
Lý thuyết về Hình trụ và khối trụ
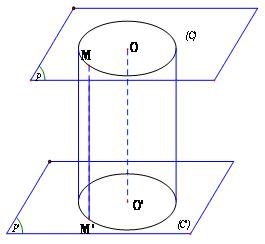
Cắt mặt trụ (T) trục Δ, bán kính R bởi 2 mặt phẳng phân biệt (P) và (P′) cùng vuông góc với Δ ta được giao tuyến là 2 đường tròn (C) và (C′).
Ta có: Phần mặt trụ (T) nằm giữa 2 mặt phẳng (P) và (P′) cùng với 2 hình tròn xác định bởi (C) và (C′) được gọi là hình trụ
- Hai đường tròn (C) và (C′) được gọi là 2 đường tròn đáy, 2 hình tròn xác định bởi chúng được gọi là 2 mặt đáy của hình trụ, bán kính của chúng gọi là bán kính hình trụ. Khoảng cách giữa 2 mặt đáy gọi là chiều cao của hình trụ
- Nếu gọi O và O′ là tâm 2 hình tròn đáy thì đoạn OO′ gọi là trục của hình trụ
- Phần mặt trụ nằm giữa 2 đáy gọi là mặt xung quanh của hình trụ
- Với mỗi điểm M thuộc (C), có 1 điểm M′ thuộc (C′) sao cho MM′∥OO″. Các đoạn thẳng như vậy gọi là đường sinh của hình trụ.
- Hình trụ cùng với phần bên trong của nó gọi là khối trụ
Ví dụ: Cho hình trụ có bán kính R và chiều cao cũng bằng R. Một hình vuông ABCD có 2 cạnh AB và CD lần lượt là dây cung của 2 đường tròn đáy, các cạnh AD và BC không phải đường sinh của hình trụ. Tính các cạnh hình vuông đó.
Giải:
Gọi C′ là hình chiếu của C trên mặt đáy chứa AB thì AB⊥BC′ ( vì AB⊥BC). Vậy AC′ là đường kính của đường tròn đáy hay AC′=2R.
Từ các tam giác vuông ABC′ và CBC′ ta có:
BC′=AC′2−AB2=4R2−AB2BC′2=BC2−CC′2=AB2−R2
Suy ra 2AB2=5R2 hay AB=R√102
Bài tập tự luyện có đáp án
Câu 1: Khối trụ tròn xoay là
- A
- B
- C
- D
Khối trụ tròn xoay là phần không gian được giới hạn bởi một hình trụ tròn xoay kể cả hình trụ đó.