Hình phẳng giới hạn bơir y=f(x), y=g(x) và y=h(x)

Bài sau

4.8/5

Tác giả: Thầy Tùng

Đăng ngày: 11 Aug 2022

Lưu về Facebook:

Hình minh họa Hình phẳng giới hạn bơir y=f(x), y=g(x) và y=h(x)

MỤC LỤC

Lý thuyết

Bài tập

Lý thuyết về Hình phẳng giới hạn bơir y=f(x), y=g(x) và y=h(x)

Diện tích hình phẳng giới hạn bởi $y=f\left( x \right)$ , $y=g\left( x \right)$ và $y=h\left( x \right)$

Cách 1:

-Tìm hoành độ giao điểm của từng cặp đồ thị.

-Chia diện tích hình phẳng cần tính thành tổng diện tích các hình phẳng giới hạn bởi hai đồ thị.

Cách 2:

-Vẽ đồ thị của các đường cong trên cùng một hệ trục tọa độ.

-Từ đồ thị chia diện tích hình phẳng cần tính thành tổng diện tích các hình phẳng giới hạn bởi hai đồ thị.

Ví dụ: Tính diện tích hình phẳng giới hạn bởi các đường $y={{x}^{2}}+2;y=2x+1;y=4x-2$ ?

Lời giải

Ta có: ${{x}^{2}}+2=2x+1\Leftrightarrow x=1$ .

${{x}^{2}}+2=4x-2\Leftrightarrow x=2$ .

$2x+1=4x-2\Leftrightarrow x=\frac{3}{2}$ .

Diện tích hình phẳng cần tìm là $S=\int\limits_{1}^{\frac{3}{2}}{\left| {{x}^{2}}+2-2x-1 \right|\text{d}x}+\int\limits_{\frac{3}{2}}^{2}{\left| {{x}^{2}}+2-4x+2 \right|\text{d}x}=\frac{1}{12}$ .

Bài sau

Bài tập tự luyện có đáp án

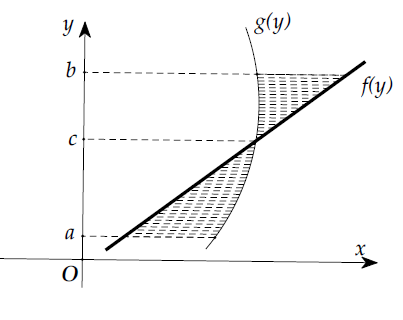
Câu 1: Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số $x=f\left( y \right)$ , $x=g\left( y \right)$ và hai đường thẳng y = a, y = b như hình vẽ bên. Khẳng định nào sau đây đúng?

A
$S=\left| \int\limits_{a}^{b}{\left[ f\left( y \right)-g\left( y \right) \right]dy} \right|$
B
$S=\int\limits_{a}^{c}{\left[ g\left( y \right)-f\left( y \right) \right]dy+\int\limits_{c}^{b}{\left[ f\left( y \right)-g\left( y \right) \right]dy}}$
C
$S=\left| \int\limits_{a}^{b}{\left[ f\left( y \right)+g\left( y \right) \right]dy} \right|$
D
$S=\int\limits_{a}^{c}{\left[ g\left( y \right)-f\left( y \right) \right]dx+\int\limits_{c}^{b}{\left[ f\left( y \right)-g\left( y \right) \right]dx}}$

Bấm vào đây để xem đáp án chi tiết

Gọi S1 là diện tích hình phẳng được giới hạn bởi x = f(y), x = g(y) và hai đường thẳng y = a, y = c $\Rightarrow {{S}_{1}}=\int\limits_{a}^{c}{\left[ g\left( y \right)-f\left( y \right) \right]dy}$

Gọi S2 là diện tích hình phẳng được giới hạn bởi x = f(y), x = g(y) và hai đường thẳng y = c, y = b $\Rightarrow {{S}_{2}}=\int\limits_{c}^{b}{\left[ f\left( y \right)-g\left( y \right) \right]dy}$

Vậy $S={{S}_{1}}+{{S}_{2}}=\int\limits_{a}^{c}{\left[ g\left( y \right)-f\left( y \right) \right]dy+\int\limits_{c}^{b}{\left[ f\left( y \right)-g\left( y \right) \right]dy}}$

Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\dfrac{-x-2}{x-1}$ , trục hoành và các đường thẳng $x=-1,x=0$ ?

A
$2$
B
$2\ln 3-1$
C
$3\ln 2-1$
D
$1$

Bấm vào đây để xem đáp án chi tiết

Diện tích hình phẳng cần tính: $S=\int\limits_{-1}^{0}{\left| \dfrac{-x-2}{x-1} \right|}dx=3\ln 2-1\left( CASIO \right)$

Câu 3: Diện tích hình phẳng giới hạn bởi các đường $y={{x}^{3}},y=0$ và hai đường thẳng $x=-1,x=2$ ?

A
$\dfrac{15}{8}$
B
$\dfrac{15}{4}$
C
$\dfrac{17}{4}$
D
$\dfrac{17}{8}$

Bấm vào đây để xem đáp án chi tiết

Diện tích hình phẳng cần tính: $S=\int\limits_{-1}^{2}{\left| {{x}^{3}} \right|dx}\to CASIO\to \dfrac{17}{4}$

Câu 4: Cho hàm số $y=f\left( x \right)$ liên tục trên đoạn $\left[ a;\,b \right]$ . Gọi $D$ là hình phẳng giới hạn bởi đồ thị hàm số $y=f\left( x \right)$ , trục hoành và hai đường thẳng $x=a,\,x=b\,\left( a < b \right)$ . Thể tích của khối tròn xoay tạo thành khi quay $D$ quanh trục hoành được tính theo công thức

A
$V=2\pi \int\limits_ a ^ b {{ f ^ 2 }\left( x \right)} d x$ .
B
$V={{\pi }^ 2 }\int\limits_ a ^ b {f\left( x \right)} d x$ .
C
$V={{\pi }^ 2 }\int\limits_ a ^ b {{ f ^ 2 }\left( x \right)} d x$ .
D
$V=\pi \int\limits_ a ^ b {{ f ^ 2 }\left( x \right)} d x$ .

Bấm vào đây để xem đáp án chi tiết

Thể tích của khối tròn xoay tạo thành khi quay $D$ quanh trục hoành được tính theo công thức $V=\pi \int\limits_ a ^ b {{ f ^ 2 }\left( x \right)} d x$ .

Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\dfrac{2}{{{\left( x+1 \right)}^{2}}}$ , trục hoành, đường thẳng $x=0$ và đường thẳng $x=4$ là:

A
$S=\dfrac{8}{5}$
B
$S=\dfrac{4}{5}$
C
$S=\dfrac{2}{25}$
D
$S=\dfrac{4}{25}$

Bấm vào đây để xem đáp án chi tiết

Diện tích hình phẳng cần tính là: $S=\int\limits_{0}^{4}{\left| \dfrac{2}{{{\left( x+1 \right)}^{2}}} \right|dx=\dfrac{8}{5}}\left( CASIO \right)$

Câu 6: Kí hiệu $S$ là diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y = f(x), y = g(x)$ và hai đường thẳng $x = a, x = b$ như hình bên. Khẳng định nào sau đây đúng?

A
$S=\int\limits_{a}^{c}{\left[ f\left( x \right)-g\left( x \right) \right]dx+\int\limits_{c}^{b}{\left[ g\left( x \right)-f\left( x \right) \right]dx}}$
B
$S=\left| \int\limits_{a}^{b}{\left[ f\left( x \right)+g\left( x \right) \right]dx} \right|$
C
$S=\int\limits_{a}^{c}{\left[ g\left( x \right)-f\left( x \right) \right]dx+\int\limits_{c}^{b}{\left[ f\left( x \right)-g\left( x \right) \right]dx}}$
D
$S=\left| \int\limits_{a}^{c}{f\left( x \right)dx+\int\limits_{c}^{b}{g\left( x \right)dx}} \right|$

Bấm vào đây để xem đáp án chi tiết

Gọi S₁ là diện tích hình phẳng được giới hạn bởi y = f(x), Ox và hai đường thẳng x = a, x = b $\Rightarrow {{S}_{1}}=\int\limits_{a}^{c}{\left[ f\left( x \right)-g\left( x \right) \right]dx}$

Gọi S₂ là diện tích hình phẳng được giới hạn bởi y = g(x), Ox và hai đường thẳng x = a, x = b $\Rightarrow {{S}_{2}}=\int\limits_{c}^{b}{\left[ g\left( x \right)-f\left( x \right) \right]dx}$

Vậy $S={{S}_{1}}+{{S}_{2}}=\int\limits_{a}^{c}{\left[ f\left( x \right)-g\left( x \right) \right]dx+\int\limits_{c}^{b}{\left[ g\left( x \right)-f\left( x \right) \right]dx}}$

Câu 7: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b như hình vẽ bên. Khẳng định nào sau đây đúng?

A
$S=\int\limits_{b}^{a}{\left| f\left( x \right) \right|dx}$
B
$S=\int\limits_{a}^{b}{f\left( x \right)dx}$
C
$S=\int\limits_{a}^{b}{\left[ -f\left( x \right) \right]dx}$
D
$S=\int\limits_{b}^{a}{f\left( x \right)dx}$

Bấm vào đây để xem đáp án chi tiết

Dựa vào nội dung ý nghĩa của tích phân ta có kết quả: $S=\int\limits_{a}^{b}{f\left( x \right)dx}$

Câu 8: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số $x=g\left( y \right)$ , trục tung và hai đường thẳng y = a, y = b như hình vẽ bên. Khẳng định nào sau đây đúng?

A
$S=\left| \int\limits_{a}^{b}{g\left( y \right)dx} \right|$
B
$S=\int\limits_{a}^{b}{g\left( y \right)dx}$
C
$S=\int\limits_{a}^{b}{g\left( y \right)dy}$
D
$S=\int\limits_{b}^{a}{\left| g\left( y \right) \right|dy}$

Bấm vào đây để xem đáp án chi tiết

Dựa vào nội dung ý nghĩa của tích phân ta có kết quả $S=\int\limits_{a}^{b}{g\left( y \right)dy}$

Câu 9: Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b như hình bên. Khẳng định nào sau đây đúng?

A
$S=\int\limits_{a}^{b}{f\left( x \right)dx-\int\limits_{a}^{b}{g\left( x \right)dx}}$
B
$S=\int\limits_{a}^{b}{f\left( x \right)dx+\int\limits_{a}^{b}{g\left( x \right)}}dx$
C
$S=\int\limits_{a}^{b}{g\left( x \right)dx-\int\limits_{a}^{b}{f\left( x \right)dx}}$
D
$S=\left| \int\limits_{a}^{b}{g\left( x \right)dx} \right|-\left| \int\limits_{a}^{b}{f\left( x \right)dx} \right|$

Bấm vào đây để xem đáp án chi tiết

Gọi S₁ là diện tích hình phẳng được giới hạn bởi y = f(x), Ox và hai đường thẳng x = a, x = b $\Rightarrow {{S}_{1}}=\int\limits_{a}^{b}{f\left( x \right)dx}$

Gọi S₂ là diện tích hình phẳng được giới hạn bởi y = g(x), Ox và hai đường thẳng x = a, x = b $\Rightarrow {{S}_{2}}=\int\limits_{a}^{b}{g\left( x \right)dx}$

Vậy $S={{S}_{1}}-{{S}_{2}}=\int\limits_{a}^{b}{f\left( x \right)dx-\int\limits_{a}^{b}{g\left( x \right)dx}}$

Câu 10: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b như hình bên. Khẳng định nào sau đây đúng?

A
$S=\left| \int\limits_{a}^{b}{f\left( x \right)}dx \right|$
B
$S=\int\limits_{a}^{c}{f\left( x \right)dx-\int\limits_{c}^{b}{f\left( x \right)dx}}$
C
$S=\int\limits_{a}^{c}{f\left( x \right)dx+\int\limits_{c}^{b}{f\left( x \right)}}dx$
D
$S=\int\limits_{a}^{b}{f\left( x \right)dx}$

Bấm vào đây để xem đáp án chi tiết

Dựa vào nội dung ý nghĩa của tích phân và chia đoạn $\left[ a;b \right]$ thành hai đoạn thành phần $\left[ a;c \right];\left[ c;b \right]$ , ta có kết quả: $S=\int\limits_{a}^{c}{f\left( x \right)dx-\int\limits_{c}^{b}{f\left( x \right)dx}}$

Câu 11: Gọi S là diện tích hình phẳng giới hạn bởi các đường $y={{e}^{x}};y=0,\,\,\,x=0,\,\,x=2$ . Mệnh đề nào dưới đây đúng?

A
$S=\int\limits_{0}^{2}{\pi {{e}^{2x}}}\text{d}x$ .
B
$S=\int\limits_{0}^{2}{{{e}^{2x}}}\text{d}x$ .
C
$S=\int\limits_{0}^{2}{\pi {{e}^{x}}}\text{d}x$ .
D
$S=\int\limits_{0}^{2}{{{e}^{x}}}\text{d}x$ .

Bấm vào đây để xem đáp án chi tiết

Theo định nghĩa, ta có $S=\int\limits_{0}^{2}{{{e}^{x}}\text{d}x}$ .

Câu 12: Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y=f\left( x \right)={{x}^{4}}-2{{x}^{2}}$ và trục hoành như hình bên. Khẳng định nào sau đây sai?

A
$S=\int\limits_{-\sqrt{2}}^{\sqrt{2}}{\left| f\left( x \right) \right|dx}$ .
B
$S=2\int\limits_{0}^{\sqrt{2}}{f\left( x \right)dx}$ .
C
$S=2\int\limits_{0}^{\sqrt{2}}{\left[ -f\left( x \right) \right]dx}$ .
D
$S=\int\limits_{-\sqrt{2}}^{0}{\left[ -f\left( x \right) \right]dx+\int\limits_{0}^{\sqrt{2}}{\left[ -f\left( x \right) \right]dx}}$ .

Bấm vào đây để xem đáp án chi tiết

Hình phẳng đối xứng qua Oy nên $S=\int\limits_{-\sqrt{2}}^{\sqrt{2}}{\left| f\left( x \right) \right|dx=2\int\limits_{-\sqrt{2}}^{0}{\left[ -f\left( x \right) \right]dx=2\int\limits_{0}^{\sqrt{2}}{\left[ -f\left( x \right) \right]dx}}}$ .

Xem thêm các bài tiếp theo bên dưới

Hình phẳng giới hạn bơir y=f(x), y=g(x) và y=h(x)

Lý thuyết về Hình phẳng giới hạn bơir y=f(x), y=g(x) và y=h(x)

Bài tập tự luyện có đáp án

Câu 1: Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số x=f(y)x=f(y) x=f\left( y \right) , x=g(y)x=g(y) x=g\left( y \right) và hai đường thẳng y = a, y = b như hình vẽ bên. Khẳng định nào sau đây đúng?

Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=−x−2x−1y=−x−2x−1 y=\dfrac{-x-2}{x-1} , trục hoành và các đường thẳng x=−1,x=0x=−1,x=0 x=-1,x=0 ?

Câu 3: Diện tích hình phẳng giới hạn bởi các đường y=x3,y=0y=x3,y=0 y={{x}^{3}},y=0 và hai đường thẳng x=−1,x=2x=−1,x=2 x=-1,x=2 ?

Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số y=2(x+1)2y=2(x+1)2 y=\dfrac{2}{{{\left( x+1 \right)}^{2}}} , trục hoành, đường thẳng x=0x=0 x=0 và đường thẳng x=4x=4 x=4 là:

Câu 6: Kí hiệu SSS là diện tích hình phẳng giới hạn bởi các đồ thị hàm số y=f(x),y=g(x)y=f(x),y=g(x)y = f(x), y = g(x) và hai đường thẳng x=a,x=bx=a,x=bx = a, x = b như hình bên. Khẳng định nào sau đây đúng?

Câu 7: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b như hình vẽ bên. Khẳng định nào sau đây đúng?

Câu 8: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số x=g(y) x=g\left( y \right) , trục tung và hai đường thẳng y = a, y = b như hình vẽ bên. Khẳng định nào sau đây đúng?

Câu 9: Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số y = f(x), y = g(x) và hai đường thẳng x = a, x = b như hình bên. Khẳng định nào sau đây đúng?

Câu 10: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số y = f(x), trục hoành và hai đường thẳng x = a, x = b như hình bên. Khẳng định nào sau đây đúng?

Câu 11: Gọi S là diện tích hình phẳng giới hạn bởi các đường y=ex;y=0,x=0,x=2 y={{e}^{x}};y=0,\,\,\,x=0,\,\,x=2 . Mệnh đề nào dưới đây đúng?

Câu 12: Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số y=f(x)=x4−2x2 y=f\left( x \right)={{x}^{4}}-2{{x}^{2}} và trục hoành như hình bên. Khẳng định nào sau đây sai?

Câu 1: Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số $x=f\left( y \right)$ , $x=g\left( y \right)$ và hai đường thẳng y = a, y = b như hình vẽ bên. Khẳng định nào sau đây đúng?

Câu 2: Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\dfrac{-x-2}{x-1}$ , trục hoành và các đường thẳng $x=-1,x=0$ ?

Câu 3: Diện tích hình phẳng giới hạn bởi các đường $y={{x}^{3}},y=0$ và hai đường thẳng $x=-1,x=2$ ?

Câu 5: Diện tích hình phẳng giới hạn bởi đồ thị hàm số $y=\dfrac{2}{{{\left( x+1 \right)}^{2}}}$ , trục hoành, đường thẳng $x=0$ và đường thẳng $x=4$ là:

Câu 6: Kí hiệu $S$ là diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y = f(x), y = g(x)$ và hai đường thẳng $x = a, x = b$ như hình bên. Khẳng định nào sau đây đúng?

Câu 8: Kí hiệu S là diện tích hình phẳng giới hạn bởi đồ thị hàm số $x=g\left( y \right)$ , trục tung và hai đường thẳng y = a, y = b như hình vẽ bên. Khẳng định nào sau đây đúng?

Câu 11: Gọi S là diện tích hình phẳng giới hạn bởi các đường $y={{e}^{x}};y=0,\,\,\,x=0,\,\,x=2$ . Mệnh đề nào dưới đây đúng?

Câu 12: Kí hiệu S là diện tích hình phẳng giới hạn bởi các đồ thị hàm số $y=f\left( x \right)={{x}^{4}}-2{{x}^{2}}$ và trục hoành như hình bên. Khẳng định nào sau đây sai?