Giao thoa sóng

Giao thoa sóng

4.6/5

Tác giả: Thầy Tùng

Đăng ngày: 11 Aug 2022

Lưu về Facebook:

Hình minh họa Giao thoa sóng

MỤC LỤC

Lý thuyết về Giao thoa sóng

Giao thoa của hai sóng phát ra từ hai nguồn sóng kết hợp ${{S}_{1}},{{S}_{2}}$ cách nhau một khoảng l:

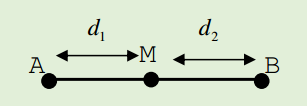
Xét điểm M cách hai nguồn lần lượt ${{d}_{1}},{{d}_{2}}$

Phương trình sóng tại 2 nguồn ${{u}_{1}}=\text{Acos}(2\pi ft+{{\varphi }_{1}})$ và ${{u}_{2}}=\text{Acos}(2\pi ft+{{\varphi }_{2}})$

Phương trình sóng tại M do hai sóng từ hai nguồn truyền tới:

${{u}_{1M}}=\text{Acos}(2\pi ft-2\pi \dfrac{{{d}_{1}}}{\lambda }+{{\varphi }_{1}})$ và ${{u}_{2M}}=\text{Acos}(2\pi ft-2\pi \dfrac{{{d}_{2}}}{\lambda }+{{\varphi }_{2}})$

Phương trình giao thoa sóng tại M: ${{u}_{M}}={{u}_{1M}}+{{u}_{2M}}$

${{u}_{M}}=2Ac\text{os}\left[ \pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\dfrac{\Delta \varphi }{2} \right]c\text{os}\left[ 2\pi ft-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda }+\dfrac{{{\varphi }_{1}}+{{\varphi }_{2}}}{2} \right]$

Biên độ dao động tại M: ${{A}_{M}}=2A\left| c\text{os}\left( \pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\dfrac{\Delta \varphi }{2} \right) \right|$ với $\Delta \varphi =\left| {{\varphi }_{1}}-{{\varphi }_{2}} \right|$

Pha dao ban đầu $\varphi = - \pi \dfrac{{{d_1} + {d_2}}}{\lambda } + \dfrac{{{\varphi _1} + {\varphi _2}}}{2}$

Bài tập tự luyện có đáp án

Câu 1: Trong thí nghiệm giao thoa sóng nước, hai nguồn kết hợp cách nhau một đoạn d dao động với phương trình ${{u}_{1}}=-{{u}_{2}}=a\cos \left( \omega t \right).$ Phương trình sóng tại điểm M nằm ở trung điểm AB là:

A
${{u}_{M}}=0.$
B
${{u}_{M}}=2a\cos \left( \omega t-\dfrac{d}{2\lambda } \right)$
C
${{u}_{M}}=2a\cos \left( \omega t-2\dfrac{d}{\lambda } \right)$
D
${{u}_{M}}=2a\cos \left( \omega t-\dfrac{d}{\lambda } \right)$

Bấm vào đây để xem đáp án chi tiết

Hai nguồn ngược pha nên M nằm ở trung điểm không dao động.

Câu 2: Chọn câu đúng. Trong quá trình giao thoa sóng. Gọi $Δφ$ là độ lệch pha của hai sóng thành phần tại cùng một điểm M. Li độ dao động tổng hợp tại M trong miền giao thoa đạt giá trị nhỏ nhất khi

A
$Δφ = (2n + 1)π/2$ .
B
$Δφ = 2nπ$ .
C
$Δφ = (2n + 1)λ$ .
D
$Δφ = (2n + 1)π$ .

Bấm vào đây để xem đáp án chi tiết

Li độ dao động tổng hợp đạt giá trị nhỏ nhất khi hai dao động ngược pha nhau hay
$Δφ = (2n + 1)π$ .

Câu 3: Hai nguồn kết hợp dao động với phương trình ${{u}_{1}}={{u}_{2}}=a\cos \left( \omega t \right).$ Phương trình sóng tại điểm M cách 2 nguồn những đoạn lần lượt là ${{d}_{1}}$ và ${{d}_{2}}$ là

A
${{u}_{M}}=2a\cos \left( \pi \dfrac{{{d}_{2}}-{{d}_{1}}}{\lambda } \right)\cos \left( \omega t+\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda } \right)$
B
${{u}_{M}}=2a\cos \left( \pi \dfrac{{{d}_{2}}-{{d}_{1}}}{\lambda } \right)\cos \left( \omega t-\pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda } \right)$
C
${{u}_{M}}=2a\cos \left( \pi \dfrac{{{d}_{2}}-{{d}_{1}}}{\lambda } \right)\cos \left( \omega t+\pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda } \right)$
D
${{u}_{M}}=2a\cos \left( \pi \dfrac{{{d}_{2}}-{{d}_{1}}}{\lambda } \right)\cos \left( \omega t-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda } \right)$

Bấm vào đây để xem đáp án chi tiết

Phương trình sóng từ nguồn 1 đến M có dạng: ${{u}_{1M}}=a\cos \left( \omega t-2\pi \dfrac{{{d}_{1}}}{\lambda } \right)$

Phương trình sóng từ nguồn 2 đến M có dạng: ${{u}_{2M}}=a\cos \left( \omega t-2\pi \dfrac{{{d}_{2}}}{\lambda } \right)$

Phương trình sóng tại M: ${{u}_{M}}={{u}_{1M}}+{{u}_{2M}}=2a\cos \left( \pi \dfrac{{{d}_{2}}-{{d}_{1}}}{\lambda } \right)\cos \left( \omega t-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda } \right)$

Câu 4: Chọn câu đúng. Trong quá trình giao thoa sóng. Gọi $Δφ$ là độ lệch pha của hai sóng thành phần tại cùng một điểm M. Biên độ dao động tổng hợp tại M trong miền giao thoa đạt giá trị cực đại khi

A
$Δφ = (2n + 1)λ/2.$
B
$Δφ = (2n + 1)π/2$ .
C
$Δφ = (2n + 1)π$ .
D
$Δφ = 2nπ$ .

Bấm vào đây để xem đáp án chi tiết

Biên độ sóng tổng hợp đạt giá trị cực đại khi
$Δφ = 2nπ$ .

Câu 5: Chọn câu đúng. Trong hiện tượng giao thoa, những điểm dao động với biên độ lớn nhất thì:

A
$Δφ = (2n + 1)π$ .
B
$Δφ = nπ$ .
C
$Δ = nλ$ với $Δ = d_2 - d_1$ hoặc $d_1 - d_2$ tùy theo quy ước ban đầu
D
$Δφ = nλ$ .

Bấm vào đây để xem đáp án chi tiết

Khi những điểm dao động với biên độ lớn nhất thì $Δφ = 2nπ$ với n nhận giá trị nguyên.
⟹ $Δ = nλ$ với $Δ = d_2 - d_1$ hoặc $d_1 - d_2$ tùy theo quy ước ban đầu

Câu 6: Hai nguồn kết hợp cách nhau một đoạn d dao động với phương trình ${{u}_{1}}={{u}_{2}}=a\cos \left( \omega t \right).$ Phương trình sóng tại điểm M nằm ở trung điểm AB là:

A
${{u}_{M}}=2a\cos \left( \omega t-\dfrac{d}{2\lambda } \right)$
B
${{u}_{M}}=2a\cos \left( \omega t-\dfrac{\pi d}{\lambda } \right)$
C
${{u}_{M}}=2a\cos \left( \omega t+\dfrac{d}{\lambda } \right)$
D
${{u}_{M}}=2a\cos \left( \omega t-2\dfrac{d}{\lambda } \right)$

Bấm vào đây để xem đáp án chi tiết

M nằm ở trung điểm AB nên cách 2 nguồn những đoạn ${{d}_{1}}={{d}_{2}}=\dfrac{d}{2}$

Phương trình sóng tại M: ${{u}_{M}}=2a\cos \left( \omega t-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda } \right)=2a\cos \left( \omega t-\dfrac{\pi d}{\lambda } \right)$

Câu 7: Điều kiện để hai sóng cơ khi gặp nhau, giao thoa được với nhau là hai sóng phải xuất phát từ hai nguồn dao động

A
có cùng pha ban đầu và cùng biên độ.
B
cùng tần số, cùng phương và có hiệu số pha không đổi theo thời gian.
C
cùng biên độ và có hiệu số pha không đổi theo thời gian.
D
cùng tần số, cùng phương.

Bấm vào đây để xem đáp án chi tiết

Điều kiện để hai sóng cơ khi gặp nhau, giao thoa được với nhau là hai sóng phải xuất phát từ hai nguồn dao động phải là 2 nguồn kết hợp.

Hai nguồn kết hợp là 2 nguồn dao động cùng phương, cùng tần số và có hiệu số pha không đổi theo thời gian.

Câu 8: Hai nguồn kết hợp dao động với phương trình ${{u}_{1}}=-{{u}_{2}}=a\cos \left( \omega t \right).$ Phương trình sóng tại điểm M cách 2 nguồn những đoạn lần lượt là d₁ và d₂ là

A
${{u}_{M}}=2a\cos \left( \pi \dfrac{{{d}_{2}}+{{d}_{1}}}{\lambda }+\dfrac{\pi }{2} \right)\cos \left( \omega t-\pi \dfrac{{{d}_{1}}-{{d}_{2}}}{\lambda }+\dfrac{\pi }{2} \right)$
B
${{u}_{M}}=2a\cos \left( \pi \dfrac{{{d}_{2}}-{{d}_{1}}}{\lambda }+\dfrac{\pi }{2} \right)\cos \left( \omega t-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda }+\dfrac{\pi }{2} \right)$
C
${{u}_{M}}=2a\cos \left( \pi \dfrac{{{d}_{2}}+{{d}_{1}}}{\lambda }+\dfrac{\pi }{2} \right)\cos \left( \omega t-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda }+\dfrac{\pi }{2} \right)$
D
${{u}_{M}}=2a\cos \left( \pi \dfrac{{{d}_{2}}-{{d}_{1}}}{\lambda }+\dfrac{\pi }{2} \right)\cos \left( \omega t-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda }-\dfrac{\pi }{2} \right)$

Bấm vào đây để xem đáp án chi tiết

Viết lại phương trình: ${{u}_{2}}=a\cos \left( \omega t\pm \pi \right).$

Phương trình sóng từ nguồn 1 đến M có dạng: ${{u}_{1M}}=a\cos \left( \omega t-2\pi \dfrac{{{d}_{1}}}{\lambda } \right)$

Phương trình sóng từ nguồn 2 đến M có dạng: ${{u}_{2M}}=a\cos \left( \omega t-2\pi \dfrac{{{d}_{2}}}{\lambda }\pm \pi \right)$

Phương trình sóng tại M: ${{u}_{M}}=2a\cos \left( \pi \dfrac{{{d}_{2}}-{{d}_{1}}}{\lambda }\mp \dfrac{\pi }{2} \right)\cos \left( \omega t-\pi \dfrac{{{d}_{1}}+{{d}_{2}}}{\lambda }\pm \dfrac{\pi }{2} \right)$

Xem thêm các bài tiếp theo bên dưới