Điều kiện để có sóng dừng trên sợi dây dài l
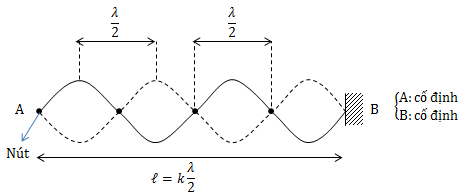
Lý thuyết về Điều kiện để có sóng dừng trên sợi dây dài l
* Hai đầu cố đinh ( hoặc tự do): l=kλ2 (k∈N∗)
λmax⇔k=1⇒ℓ=λmax2⇔λmax=2ℓ
Số bụng sóng = số bó sóng = k
Số nút sóng = k + 1
* Một đầu cố định và một đầu tự do: l=(2k+1)λ4 (k∈N)
λmax⇔k=0⇒ℓ=λmax4⇔λmax=4ℓ
Số bó sóng nguyên = k
Số bụng sóng = số nút sóng = k + 1
Bài tập tự luyện có đáp án
Câu 1: Khi có sóng dừng trên một sợi dây đàn hồi thì khoảng cách giữa hai bụng sóng liên tiếp bằng
- A
- B
- C
- D

Trong sóng dừng thì độ dài của một bó sóng bằng λ2 . Mà khoảng cách giữa hai bụng sóng liên tiếp chính bằng độ dài của một bó sóng và bằng λ2 (nửa bước sóng).
Câu 2: Một dây đàn hồi có chiều dài ℓ, hai đầu cố định. Sóng dừng trên dây có bước sóng dài nhất là
- A
- B
- C
- D
Dây có hai đầu cố định. Sóng dừng trên dây có bước sóng dài nhất là: λ_{max} =2 ℓ.
Câu 3: Câu nào sau đây là sai khi nói về sóng dừng?
- A
- B
- C
- D
Điều kiện L=(k+1)\dfrac{\lambda }{2} chỉ là điều kiện để xảy ra sóng dừng trên dây với hai đầu cố định. Với trường hợp một đầu cố định, một đầu tự do thì điều kiện sẽ là L=(2k+1)\dfrac{\lambda }{4} .
Câu 4: Để có hiện tượng sóng dừng trên một sợi dây, một đầu cố định, một đầu tự do, thì chiều dài của sợi dây thoả mãn ( k\in Z )
- A
- B
- C
- D
Điều kiện để xảy ra sóng dừng đối với dây có một đầu cố định, một đầu tự do là với m là số lẻ. Hoặc có thể viết cách khác L=\left( 2k+1 \right)\dfrac{\lambda }{4} với k là số nguyên.
Câu 5: Một sợi dây đàn hồi được treo thẳng đứng vào một điểm cố định, đầu còn lại thả tự do. Người ta muốn tạo ra sóng dừng trên dây thì tần số thỏa mãn điều kiện nào sau đây.
- A
- B
- C
- D
Vì một đầu dây cố định và một đầu tự do nên.
\ell =\left( 2k+1 \right)\dfrac{\lambda } 4 =\left( 2k+1 \right)\dfrac{v}{{}4f}\Rightarrow f=\left( 2k+1 \right)\dfrac{v}{{}4\ell }
Câu 6: Một dây đàn hồi có chiều dài L, một đầu cố định, một đầu tự do. Sóng dừng trên dây có bước sóng dài nhất là
- A
- B
- C
- D
\ell =\dfrac{\lambda }{4}\Rightarrow {{\lambda }_{\text{max}}}=4\ell \ell =\dfrac{\lambda }{4}\Rightarrow {{\lambda }_{\text{max}}}=4\ell
Câu 7: Một sợi dây đang có sóng dừng ổn định. Bước sóng của sóng truyền trên dây là \lambda . Hai đểm nút liên tiếp cách nhau :
- A
- B
- C
- D
Hai nút liên tiếp cách nhau một nửa bước sóng.
Câu 8: Sóng dừng xảy ra trên dây đàn hồi với hai đầu là nút khi
- A
- B
- C
- D
Điều kiện để có sóng dừng trên một sợi dây có hai đầu cố định là: L=n\dfrac{\lambda }{2} (Với n là một số nguyên).
Câu 9: Trên một sợi dây đàn hồi đang có sóng dừng với bước sóng \lambda . Khoảng cách từ một nút đến một bụng liền kề nó bằng
- A
- B
- C
- D

Khoảng cách của một bó sóng trong sóng dừng bằng \dfrac{\lambda }{2} . Khoảng cách từ một nút đến một bụng liền kề bằng khoảng cách của nửa bó sóng nên bằng \dfrac{\lambda }{4} .
Câu 10: Điều kiện có sóng dừng trên dây chiều dài ℓ khi cả hai đầu dây cố định hay hai đầu tự do là
- A
- B
- C
- D
Điều kiện có sóng dừng trên dây chiều dài ℓ khi cả hai đầu dây cố định hay hai đầu tự do là: ℓ = kλ/2.
Câu 11: Sóng dừng xảy ra trên dây đàn hồi hai đầu cố định khi
- A
- B
- C
- D
Điều kiện để xảy ra sóng dừng với dây có 2 đầu cố định là \ell =k\dfrac{\lambda }{2} (với k là số nguyên).
Câu 12: Sóng truyền trên một sợi dây có một đầu cố định, một đầu tự do. Muốn có sóng dừng trên dây thì chiều dài của sợi dây phải bằng
- A
- B
- C
- D
Điều kiện để xảy ra sóng dừng đối với dây có một đầu cố định, một đầu tự do là L=m\dfrac{\lambda }{4} với m là số lẻ.
Câu 13: Điều kiện có sóng dừng trên dây chiều dài ℓ khi một đầu dây cố định và đầu còn lại tự do là
- A
- B
- C
- D
Điều kiện có sóng dừng trên dây chiều dài ℓ khi một đầu dây cố định và đầu còn lại tự do là: ℓ = (2k + 1)λ/4.
Xem thêm các bài tiếp theo bên dưới